Главная | Обратная связь

Непрерывные системы

Задачи оптимального управления непрерывными детерминированными системами делятся на два класса:

Задачи, в которых функции управления u_i(t) неограничены и являются непрерывными во времени (задачи Лагранжа).

Задачи, в которых функции управления u_i(t) имеют ограничения и на интервале управления претерпевают разрывы первого рода, т.е. имеющих в точках разрыва конечные пределы слева и справа (задачи Понтрягина).

Введем понятие траекторий управляемых процессов и рассмотрим построение этих траекторий.

Пусть имеется управляемый процесс, описываемый в пространстве состояний системой дифференциальных уравнений

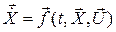, (П.6.1)

где

f_i – известные функции.

Заданы также интервал управления t = 0 ¸ T и начальное состояние системы .

Если задать программу управления для непрерывного вектора , то этой программе будет соответствовать определенная траектория вектора состояния . Чтобы найти , нужно подставить известный вектор в (П.6.1) и решить для этого векторного уравнения задачу Коши с заданным начальным условием Такое решение X(t) в силу непрерывности будет существовать. Построенные на графике зависимости x_i(t) на интервале t = 0 ¸ T будут представлять траектории процесса во времени. Если число переменных состояния равно двум, то траектории процесса можно представить на плоскости с координатами x₁, x₂, называемой фазовой плоскостью. Если число переменных состояния больше двух, то траектории процесса могут быть представлены в многомерном фазовом пространстве с координатами x₁, x₂, x₃ ¼ .

Рассмотрим теперь случай, когда управление - разрывная функция. Будем в качестве допустимых считать такие управления, которые имеют на интервале управления t = 0 ¸ T конечное число точек разрыва первого рода (рис.1.а). Пусть терпит разрывы в точках t₁, t₂ ¼ t_k < T.

 

Рис. П.6.1. Траектория управляемого процесса во времени

при разрывной функции управления

 

Тогда в этих точках существуют односторонние пределы (пределы слева и справа)

 

Чтобы однозначно задавать значения в точках разрыва, потребуем, чтобы была непрерывна справа. Тогда и график ее (для одной составляющей вектора) будет выглядеть так, как представлено на рис. 1.а. Для построения решения, соответствующего заданному закону управления, рассмотрим последовательно отрезки 0 ¸ t₁, t₁ ¸ t₂ , ¼ t_k ¸ T. На промежутке 0 ¸ t₁ функция будет непрерывна во всех точках, если дополнить ее значением при t = t₁, равным пределу слева. Тогда на этом промежутке времени будет определена траектория , отвечающая заданной функции и начальному условию

Рассмотрим теперь отрезок t₁ ¸ t₂. Если на нем доопределить функцию в точке t₁ пределом справа, а в точке t₂ пределом слева, она также будет непрерывна. Если в качестве начального условия взять конечное состояние , то мы слева получим траекторию системы. Продолжая этот процесс, мы в итоге получим траекторию на всем интервале управления.

Отметим некоторые свойства построенной траектории . Во-первых, эта траектория, как следует из правила ее построения, однозначно соответствует заданным управлению и начальному условию, поэтому ее можно считать обобщением решения задачи Коши на случай разрывных управлений. Во-вторых, полученное решение будет непрерывным. В-третьих, на каждом интервале (t_i, t_i+1) имеет непрерывную производную в любой точке, а в точках разрыва t_i – производную слева и справа. Производная этой функции, следовательно, будет кусочно-непрерывна.

В качестве примера рассмотрим управляемую систему, заданную системой уравнений

 

на промежутке 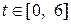. Начальные значения переменных x₁(0) = x₁₀ , x₂(0) = x₂₀ примем равными x₁₀ = 1, x₂₀ = -1, а управления зададим в виде

 

Точки разрыва управлений делят отрезок [0, 6] на три части точками t₁ = 2, t₂ = 4. Эти точки и являются точками разрыва управления.

Рассмотрим промежуток [0, 2]. При таких значениях t управления имеют значения u₁ = 0, u₂ = -1. Система после подстановки имеет вид

 

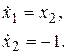
Начальные условия на этом промежутке заданы условием задачи.

Найдем общее решение полученной системы:

 

Подставляя сюда начальные условия, найдем значения произвольных постоянных с₁ = -1, с₂ = 1. Следовательно, траектория системы на рассматриваемом промежутке имеет вид

Определим отсюда начальное значение x₁(2) = x₁₂ , x₂(2) = x₂₂ на следующем промежутке [2, 4]. Для этого нужно подставить t = 2 в полученные выражения для x₁ , x₂. Начальными значениями будут x₁₂ = - 3, x₂₂ = - 3.

Система уравнений процесса, которой удовлетворяет искомая траектория, на этом промежутке будет следующей:

 

Общее решение x₁ = C₁t + C₂ , x₂ = C₁ после подстановки начальных условий даст уравнение траектории на промежутке [2, 4]:

откуда получим x₁(4) = x₁₄ = - 9, x₂(4) = x₂₄ = - 3.

Наконец, траектория на участке [4, 6] определяется как решение системы

 

откуда с учетом найденных начальных значений x₁₄ , x₂₄ получим

.

Окончательно полученная траектория, отображенная на рис. П.6.2, имеет вид

 

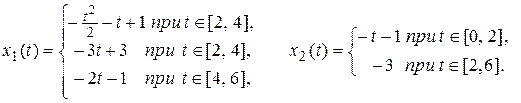
Графическое представление траекторий управляемой системы часто дает ценную информацию для решения задач управления. Изображение траекторий на плоскости 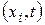, как сделано на рис. П.6.2, - один из возможных способов их графического представления. Иногда более информативным бывает представление траекторий на фазовой плоскости (x₁, x₂).

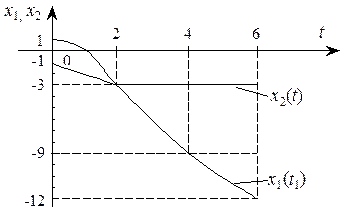
Рис. П.6.2. Траектория управляемого процесса во времени

Рассмотрим в качестве примера систему второго порядка

 

и изобразим на фазовой плоскости все ее траектории для значений управления u₁ = - 1, u₂ = 1. Подставляя эти значения управлений в уравнения процесса, после подстановки получаем и находим общее решение полученной системы:

 

Эти уравнения задают в параметрическом виде искомое семейство траекторий. Параметр t можно исключить, перенося единицу в левую часть и сложив возведенные в квадрат части уравнений:

.

Теперь видно, что кривые данного семейства – окружности радиусом с центром в точке (1, 1).

Аналогично можно построить семейство кривых, отвечающих значению управления u₁ = 1, u₂ = - 1. Проводя такие же вычисления, получим уравнение в виде , т.е. семейство окружностей с центром в точке (-1, -1).

На фазовой плоскости системы оба семейства траекторий изображены на рис. П.6.3. Стрелками показано направление движения точки по траектории при возрастании t.

Рис. П.6.3. Траектория управляемого процесса на фазовой плоскости

С помощью построений можно решать более сложные задачи, например, построение траекторий, отвечающих кусочно-постоянным управлениям. Это часто бывает необходимо в задачах оптимального управления.

Например, пусть известно начальное состояние системы

и требуется отыскать траекторию системы, отвечающую на промежутке времени управлениям

 

При управления будут иметь значения u₁ = - 1, u₂ = 1. Так как мы уже построили все множество траекторий с такими значениями управлений, остается выяснить, какая из них проходит через начальную точку (2, 1). Мы знаем, что это окружность, следовательно, нужно определить ее радиус. Это нетрудно сделать, заметив, что он равен расстоянию от точки (2, 1) до центра, т.е. точки (1, 1). Это расстояние и вместе с ним радиус r = 1. Таким образом, на первом участке траектория системы – дуга окружности радиусом r = 1 с центром в точке (1, 1). Далее мы можем воспользоваться следующим из формул для x₁ и x₂ соображением, что радиус-вектор точки траектории, проведенной из ее центра, за промежуток времени описывает угол, численно равный длительности промежутка. Следовательно, радиус-вектор по отношению к начальному состоянию в конце промежутка [0, p2] поворачивается на угол p2.

Нетрудно видеть (рис. П.6.4), что тогда при система оказывается в состоянии . Теперь, пользуясь изложенными соображениями, можно построить участок траектории на промежутке [p2, 3p2]. Этот участок – половина дуги окружности радиусом с центром в точке (-1, -1).

Рис. П.6.4. Траектория управляемого процесса на фазовой плоскости при кусочно-постоянном управлении

Дискретные системы

В качестве примера построения траекторий управляемых процессов для дискретных систем рассмотрим систему, описываемую однородным разностным уравнением второго порядка вида

x(n + 1) = u(n) x(n) – x(n – 1),

где u(n) – управляющее воздействие, n – номер цикла.

Зададим ограничение на управление - 2 £ u £ 2 и начальные условия x(0), x(-1), например x(0) = 0,7; x(-1) = 0. При этих условиях по уравнению вычислим x(1), x(2), x(3) и т.д.

На рис. П.6.5 приведены траектории дискретного процесса x(n) от номера цикла n при постоянных значениях управляющего воздействия u = 0,5 и u = 1.

Из этого рисунка видно, что дискретные значения x(n) представляют отсчеты из гармонического колебания постоянной амплитуды, частота которого зависит от управляющего воздействия u.

Если построить эту траекторию на фазовой плоскости с координатами x(n) и x(n - 1) (фазовый портрет), то эта траектория в зависимости от величины управляющего воздействия будет иметь вид эллипсов, представленных на рис. П.6.6.

При u = 0 эллипс превращается в окружность.

Рис. П.6.5. Траектория дискретного процесса при постоянных значениях u

Рис. П.6.6. Траектории дискретного процесса на фазовой

плоскости при различных значениях u

На рис. П.6.7 приведены траектории дискретного процесса при двух фиксированных значениях управляющего воздействия: при и при u = 1.

 

Рис. П.6.7. Траектории дискретного процесса

при двух фиксированных значениях u

 

Из рис. П.6.7 видно, что траектории представляют собой два эллипса с наклоном главной оси этих эллипсов под углом p/4 относительно оси x(n - 1). Эти эллипсы имеют точки пересечения. Соединив эти точки прямыми через начало координат, эти прямые образуют сектора с углами a₁ и a₂ соответственно, причем a₂ = p - a₁.

Теперь построим траектории процесса при изменяющемся управляющем воздействии. Закон изменения управляющего воздействия зададим следующим: если точка на фазовой плоскости x(n), x(n - 1) попадает в сектор a₁, то устанавливаем u = 1, а если в сектор a₂, то . При таком законе изменения управляющего воздействия траектория процесса приведена на рис. П.6.8 и имеет вид раскручивающейся спирали, что свидетельствует о бесконечном возрастании амплитуды процесса x(n).

Если закон изменения управляющего воздействия задать обратным предыдущему, а именно: если точка на фазовой плоскости x(n), x(n - 1) попадает в сектор a₁, то устанавливаем , а если в сектор a₂, то u = 1. При таком законе управления траектория процесса приведена на рис. П.6.9 и имеет вид сворачивающейся к началу координат спирали.

Рис. П.6.8. Траектория дискретного процесса

в виде раскручивающейся спирали

Рис. П.6.9. Траектория дискретного процесса

в виде сворачивающейся спирали

Отметим, что разностное уравнение второго порядка вида x(n + 1) = u× x(n) – - x(n - 1) можно представить в виде системы из двух связанных разностных уравнений первого порядка

x₁(n + 1) = x₁(n) – u₁ x₂(n)

x₂(n + 1) = x₂(n) + u₁ x₁(n + 1),

где u₁ – управляющее воздействие.

Траектория процесса в этом случае описывается в координатах x₁ и x₂.

Для определения связи между управляющими воздействиями u и u₁ преобразуем эту систему в одно разностное уравнение второго порядка. Для этого подставим во второе уравнение значение x₁(n + 1) из первого уравнения. В результате получим

x₂(n + 1) = x₂(n) + u₁ x₁(n) – u₁² x₂(n).

Из второго уравнения системы на предыдущем такте имеем: x₂(n + 1) = = x₂(n - 1) + u₁ x₁(n), откуда выразим значение x₁(n): . Подставим это выражение в приведенное выше уравнение и получим разностное уравнение второго порядка

x₂(n + 1) = (2 - u₁²) x₂(n) - x₂(n - 1).

Сопоставляя это уравнение с исходным, получим следующие соотношения между воздействиями u и u₁: u = 2 - u₁², .

Построение траекторий управляемых процессов дает о них наглядное графическое представление и позволяет определить, как от управляющего воздействия зависит вид траекторий и их характерные особенности.