Главная | Обратная связь

Приложение 9. Постановка и решение задачи оптимального управления непрерывными процессами методом ДП в общем виде

 

Пусть задана оптимизационная задача для непрерывного процесса, описываемого системой из m дифференциальных уравнений вида:

. (П.9.1)

где f_i – известные функции,

- вектор состояния (1 ´ m),

- вектор управления (1 ´ r).

Заданы начальное состояние системы 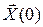, допустимые пространства состояний и управлений 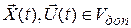, интервал управления t = 0 ¸ T и выражение для целевой функции вида:

(П.9.2)

где f₀, F – подынтегральная и терминальная функции соответственно. Необходимо найти оптимальный вектор управления на интервале t = 0 ¸ T, чтобы обеспечить (П.9.2).

Для решения задачи оптимального управления непрерывными системами методом динамического программирования (ДП) введем функцию Беллмана являющуюся функцией m + 1 переменной (m переменных вектора и одна переменная – время). Отличительной особенностью функции является то, что она не должна зависеть от переменных вектора управления

Затем с помощью функции Беллмана построим две новые функции и (в литературе их называют иногда формальными функциями) по соотношениям:

(П.9.3)

. (П.9.4)

Поставленная оптимизационная задача решается методом ДП при таком векторе управления который формирует процесс , максимизирующий функцию на всем интервале управления t = 0 ¸ T, то есть

(П.9.5)

а также минимизирует функцию при t = T, т.е. в конце процесса управления. При 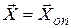оптимальный вектор управления . Отметим, что функция может быть представлена через функцию Гамильтона Н в виде:

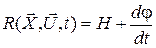, (П.9.6)

где (П.9.7)

функция Гамильтона, в которой частные производные выступают в роли присоединенных функций.

С учетом (П.9.6) выражение (П.9.5) примет вид:

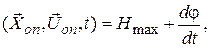(П.9.8)

откуда: , (П.9.9)

где - процесс при максимальной функции Гамильтона.

Из (П.9.9) получим:

. (П.9.10)

Это уравнение Гамильтона–Якоби–Беллмана для непрерывных процессов. При = 0 как частный случай из него следует уравнение Беллмана

,

в которое входит производная функции Беллмана по времени. Граничные условия для уравнений (П.9.9) и (П.9.10) определяются из (П.9.4), откуда следует :

, (П.9.11)

где

При имеем:

(П.9.12)

Из (П.9.9) и (П.9.10) следует, что решение этих уравнений с граничными условиями (П.9.11) и (П.9.12) есть задача Коши.

Основной проблемой применения метода ДП для непрерывных процессов является отыскание функции . Универсальных алгоритмов поиска этой функции не существует.

 

Список литературы

1. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М.: Наука, 1979.

2. Беллман Р. Динамическое программирование. М.: Изд-во иностр. лит., 1960.

3. Беллман Р. Методы вычислений // Автоматика и телемеханика. 1993. № 8. С. 10.

4. Брокате М. Оптимальное управление системами гистерезисного типа // Автоматика и телемеханика. 1991. № 12; 1992. № 1.

5. Винер Н. Кибернетика и общество. М.: Изд-во иностр. лит., 1958.

6. Интрилигатор М. Математические методы оптимизации и экономическая теория/Пер. с англ. - М.: Айрис-пресс, 2002. - 576 с.: ил. - (Высшее образование).

7. Колемаев В.А. Математическая экономика: Учебник для вузов. - 2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2002. - 399 с.

8. Красовский Н.Н. Теория управления движением. М.: Наука, 1968.

9. Лагоша Б.А. Оптимальное управление в экономике: теория и приложение: учеб. Пособие. – 2-е изд., перераб. И доб. / Б.А. Лагоша, Т.Г. Апалькова. – М.: Финансы и статистика, 2008. – 224 с.:ил.

10. Лагоша Б.А. Оптимальное управление в экономике: Учеб. пособие. - М.: Финансы и статистика, 2003. - 192 с.: ил.

11. Основы теории оптимального управления: Учеб. пособие для экон. вузов/В.Ф.Кротов, Б.А.Лагоша, С.М.Лобанов, и др.; Под ред. В.Ф.Кротова. - М.: Высш. шк., 1990. - 430 с.: ил.

12. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1969.

13 Ройтенберг Я.Н. Гироскопы. М.: Наука, 1975.

14. Рудик А.П. Ядерные реакторы и принцип максимума Понтрягина. М.: Атомиздат, 1970.

15. Черноусько Ф.Л., Колмановский В.Б. Вычислительные и приближенные методы оптимального управления // Итоги науки и техники. Мат. анализ. 1977. Т. 14..

16. Шимко П.Д. Оптимальное управление экономическими системами :учеб.пособие для вузов. - СПб.: Бизнес-пресса, 2004 Гриф МО

17. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов/В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. - М.: ЮНИТИ, 2002. - 391 с.

18. Afanasiev V.N., Kolmanovskii V.B., Nosov V.R. Mathematical Theory of Control Systems Design. Dordrecht: Kluwer, 1996.

19. Swan G.W. Application of Control Theory in Medicine. N.Y.: Dekker, 1984.

 

[1] Обратная матрица рассчитана на ПК с помощью Excel

[O1]