 |
|
Применение метода ДП для поиска оптимального управления предприятием
Экономическая модель предприятия в непрерывном времени описывается уравнением движения капитала:
, (П.3.1)
где K - стоимость основных производственных фондов, I - инвестиции на обновление ОПФ, m - коэффициент амортизации ОПФ.
Из однопродуктовой модели имеем:
I = Y – C , где Y = X – W = X – aX = (1 – a) X, X - произведенный продукт, Y - конечный продукт, 0 < а < 1 - доля продукта, идущая в производство, C - непроизводственное потребление.
Введем управление 
, показывающее, какая доля конечного продукта (в денежных единицах) направляется на непроизводственное потребление в виде зарплаты, премий и т.д. для людей, работающих на предприятии, причем 0 < u <1.
Тогда I = (1 – u) Y = (1 – a) (1- u) X . (П.3.2)
Подставим это выражение в (П.3.1) и получим дифференциальное уравнение, описывающее движение ОПФ предприятия
. (П.3.3)
Заданы начальное условие K(0), ограничение на управление 0 £ u £ 1 и интервал управления t = 0 ¸ T. В качестве целевой функции выберем интегральное среднедушевое непроизводственное потребление каждого сотрудника предприятия на продолжительном интервале управления t = 0 ¸ T, выражаемое формулой:
, (П.3.4)
где L - количество работающих на предприятии.
Известно, что при большом интервале управления T происходит дисконтирование (обесценивание) с годами заработанных средств. Для учета этого процесса введем в целевую функцию фактор дисконтирования, тогда она примет вид:
, (П.3.5)
где d - коэффициент дисконтирования.
Введем в исходное уравнение (П.3.3), описывающее модель предприятия, относительные переменные 
- фондовооруженность, 
- среднедушевое непроизводственное потребление, 
- производительность труда на предприятии. Тогда с учетом новых (относительных) переменных получим из (П.3.3)
Так как 
, где 
прирост трудовых ресурсов, n - коэффициент, характеризующий прирост или спад трудовых ресурсов. Тогда 
Подставим это выражение в исходное уравнение, разделим левую и правую части на L и получим
(П.3.6)
Для описания нормированной модели введем также нормированную производственную функцию Кобба-Дугласа
где 
- функция Кобба-Дугласа.
Начальные условия на стоимость ОПФ заменим на начальное условие фондовооруженности 
. Для нормированных переменных целевая функция примет вид:
, (П.3.7)
т. к. 
Из выражений (П.3.6) и (П.3.7) следует, что в нормированной оптимизационной задаче состоянием системы являются фондовооруженность k , а управлением являются нормированная функция производства 
и доля непроизводственного среднедушевого потребления u, то есть произведение x× u.
Решение поставленной задачи будем искать методом ДП. Для приведения ее к классическому виду, когда ищется минимум целевой функции, вместо функции
(П.3.7) введем новую целевую функцию:
. (П.3.8)
Функция R с учетом (П.3.6) и (П.3.8) примет вид:
.
Чтобы функция j не зависела от управления x× u, выделим в функции R слагаемые, зависящие от x× u, и приравняем сумму коэффициентов при них нулю. В результате, получим уравнение:
откуда 
или 
Решение этого уравнения имеет вид 
Положим для простоты 
и получим 
Тогда 
При полученных выражениях 
и 
функция R не будет зависеть от управления u и примет вид:
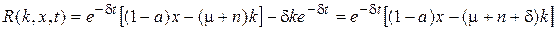(П.3.9)
Оптимальные процессы 
и 
найдем из условия:
Так как a < 1, то (1 – a) > 0, следовательно максимум R по x достигается при 
Теперь проведем максимизацию R по k при 
Так как 
не зависит от k, то вместо R введем более простую функцию 
вида:
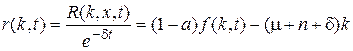(П.3.10)
и будем искать оптимальную фондовооруженность из условия 
Вначале исследуем функцию графически.
На рис. П.3.1 приведена зависимость от k при 
вида (П.3.11).
Рис. П.3.1. Зависимость функции от k
Из этого рисунка видно, что функция имеет максимум 
при 
.
Найдем это значение .
Для этого введем нормированную производственную функцию Кобба-Дугласа вида:
, (П.3.11)
где b - параметр нормированной функции Кобба-Дугласа,
r - коэффициент, характеризующий темпы роста научно-технического прогресса,
a - коэффициент эластичности по фондам.
Необходимым условием максимизации 
по k является (см. рис. П.3.1) равенство нулю производной 
т. е. 
Так как 0 < a < 1, то из этого уравнения получим:
. (П.3.12)
Это уравнение оптимальной фондовооруженности предприятия по критерию (П.3.5) называется магистралью. График зависимости магистрали от времени t приведен на рис. П.3.2.
Рис. П.3.2. График зависимости оптимальной фондовооруженности предприятия от времени
Для определения оптимального управления 
предприятием возьмем производную 
от уравнения магистрали (П.3.12) и получим:
(П.3.13)
Подставим это выражение в дифференциальное уравнение (П.3.6), описывающее нормированную модель предприятия и с учетом (П.3.11) получим:
. (П.3.14)
Так как 
то после подставки этого выражения в (П.3.14) окончательно получим:
(П.3.15)
Из этого выражения видно, что оптимальное управление 
в данной модели не зависит от времени и при условии 
определяется как 
где 
коэффициент эластичности по труду.
Приложение 4.