Главная | Обратная связь

Приложение 7. Поиск оптимального управления непрерывными детерминированными процессами методами Лагранжа-Понтрягина

 

В общем виде управляемая динамическая система описывается системой дифференциальных уравнений первого порядка вида

, (П.7.1)

где x_i – переменные состояния системы,

u_j – управляющие воздействия,

f_i – известные функции,

.

Заданы также интервал управления t = 0 ¸ T и начальное состояние системы .

Необходимо определить управляющий вектор 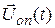, при котором в определенном смысле достигается наилучший результат, например, нужно минимизировать функционал вида

. (П.7.2)

 

Пусть непрерывные функции f_i , f₀ и F непрерывно дифференцируемы по x_i и u_j. Если на управляющие воздействия не накладываются ограничения, то такая задача нахождения оптимального управления принадлежит классу вариационного исчисления и относится к задаче Лагранжа.

Если на управляющие воздействия u_j накладываются ограничения двух видов:

управляющие воздействия могут изменяться в допустимых пределах ½u_j½£ u_доп ,

управляющие воздействия могут претерпевать разрывы первого рода, -

то такая задача нахождения оптимального управления может быть решена с использованием принципа максимума Понтрягина.

В методе Лагранжа для решения оптимизационной задачи вводятся два вида вспомогательных функций:

функция Гамильтона, определяемая по выражению

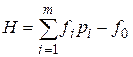, (П.7.3)

 

где f_i – функции в выражении (П.7.1),

f₀ – подынтегральная функция в выражении (П.7.2),

p_i – присоединенные функции, определяемые в результате решения следующей системы дифференциальных уравнений:

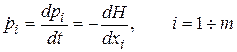, (П.7.4)

или в векторной форме:

где матрица 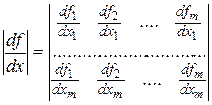разностью m ´ m.

Из (П.7.4) следует:

. (П.7.5)

 

Уравнения (П.7.4) и (П.7.5) представляют собой каноническую или гамильтонову форму записи уравнений Эйлера-Лагранжа, играющих важную роль в классическом вариационном исчислении. В теории классического вариационного исчисления доказывается следующая теорема, определяющая необходимые условия оптимальности:

при оптимальном управлении системой, описываемой (П.7.1), когда минимизируется функционал (П.7.2), обращаются в нуль частные производные 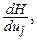то есть должны выполняться условия:

(П.7.6)

 

Для поиска вектора оптимального управления 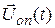методом Лагранжа необходимо вначале определить присоединенные функции p_i. Они определяются в результате решения дифференциальных уравнений (П.7.4). Для этого необходимо знать граничные условия для присоединенных функций p_i. Эти граничные условия определяются в зависимости от конкретных особенностей задачи оптимального управления.

Если требуется минимизировать функционал вида:

, (П.7.7)

 

то есть речь идет о минимизации линейной комбинации координат системы в конце процесса управления, то граничные условия для присоединенных функций определяются из выражения:

p_i(T) = - c_i , i = 1 ¸ m.

Если нужно минимизировать нелинейную функцию координат x_i(T), а именно:

J = F(x_i(T)) = min, i = 1 ¸ m,

где F – нелинейная функция, дважды дифференцируемая по всем аргументам x_i, тогда граничные условия для присоединенных функций определяются из выражений:

.

Если нужно минимизировать функционал вида:

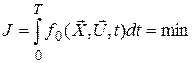, (П.7.8)

 

в котором терминальная функция F = 0, то граничные условия для присоединенных функций равны нулю в точке t = T, то есть:

p_i(T) = 0, i = 1 ¸ m.

Условие трансверсальности. Часто в задачах оптимального управления задаются определенные условия для системы в конце процесса управления, в точках x_i(T). Если вместе с основной задачей оптимального управления в виде функционала (35) должны выполняться условия в конце процесса управления, заданные в виде:

F_j(x_i(T)) = 0, j = 1 ¸ m,

причем функции F_j дважды дифференцируемы по всем x_i, тогда граничные значения для присоединенных функций при t = T определяются из условия трансверсальности

 

где 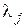- неизвестные множители Лагранжа, определяемые из граничных условий системы в конце процесса управления.

 

Пример 1. Динамическая система описывается системой дифференциальных уравнений вида:

 

Заданы также промежуток или интервал управления t = 0 ¸ 1 и начальное состояние системы x₁(0) и x₂(0). Необходимо найти оптимальное управление u_оп, при котором достигается условие

.

 

Решение. Для данного критерия оптимального управления функция Гамильтона имеет вид:

 

система присоединенных функций равна:

 

 

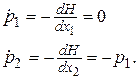
Граничные условия для присоединенных функций в этом примере равны нулю в конце процесса управления, то есть p₁(1) = 0, p₂(1) = 0, так терминальная функция в функционале J равна нулю.

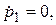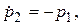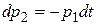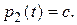Так как и то тогда , откуда так как то Но 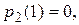следовательно

Тогда функция Гамильтона примет вид Оптимальное управление найдем из условия следовательно откуда 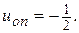Действительно, интеграл при и равен

Пример 2. Динамическая система описывается системой дифференциальных уравнений вида

 

Задано начальное состояние системы x₁(0) = 0 , x₂(0) = 0. Необходимо на интервале управления системой t = 0 ¸ 1 обеспечить два условия:

минимизировать интеграл

 

 

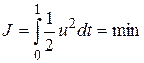
и обеспечить конечное состояние системы, заданное выражениями

, .

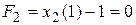Из этих выражений следуют конечные состояния координат системы x₁(1) = 1, x₂(1) = 1.

Решение. Функция Гамильтона для этого примера примет вид:

 

Присоединенные функции определим из формулы (П.7.4)

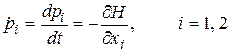
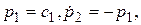и получим следовательно следовательно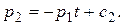

Для определения коэффициентов с₁ и с₂ воспользуемся условием трансверсальности

 

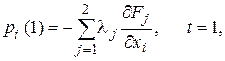
где l_j – неизвестные множители Лагранжа, обеспечивающие заданное конечное состояние системы. Из этого выражения имеем: p₁(1) = - l₁, p₂(1) = - l₂ .

Тогда p₁(t) = - l₁, p₂(t) = l₁t + c₂.

При t = 1 имеем равенство: -l₂ = l₁ × 1+ c₂, откуда c₂ = - l₁ - l₂ , тогда p₂(t) = l₁t - l₁ - l₂.

Подставим эти выражения в формулу для функции Гамильтона и получим:

 

Из условия получения оптимального управления методом Лагранжа имеем:

Откуда

Неизвестные множители l₁ и l₂ определим из условия, чтобы при t = 1 обеспечить заданное конечное состояние координат системы: x₁(1) = 1, x₂(1) = 1.

Для этого осуществим интегрирование уравнений состояния системы с учетом ее начального состояния x₁(0) = 0 и x₂(0) = 0.

Из второго уравнения имеем

.

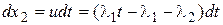После интегрирования этого выражения получим:

 

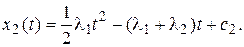
При t = 0 x₂(0) = 0, следовательно c₂ = 0.

Тогда

Подставим это выражение в первое уравнение системы и после интегрирования выражения 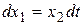получим:

 

При t = 0 x₁(0) = 0, следовательно c₁ = 0.

При t = 1 имеем x₁(1) = 1, x₂(1) = 1. Подставим в уравнения для x₁(t) и x₂(t) эти значения при t = 1 и получим:

 

 

Решение этой системы дает искомые множители Лагранжа: .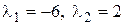

Тогда окончательный результат для оптимального управления примет следующий вид:

 

 

Траектория оптимального управления u_оп и координат x_1оп, x_2оп системы на интервале управления t = 0 ¸ 1 приведена на рис.10.

Рис. П.7.1 Траектория оптимального управления для примера 2

 

Отличие принципа максимума Понтрягина от метода Лагранжа состоит в том, что из-за ограничений на управление и наличия в управляющих функциях разрывов первого рода условия (П.7.6) в строгом математическом смысле не выполняются. Эти условия в принципе максимума Понтрягина заменяются на другое более общее положение, а именно: чтобы управляющий вектор решил поставленную оптимизационную задачу минимизировать функционал J, необходимо существование не равного тождественно нулю вектора присоединенных функций с соответствующим граничным условием, который вместе с вектором управления на всем интервале управления обеспечивал бы максимум функции Гамильтона, то есть:

. (П.7.9)

Если нужно максимизировать функционал J, то указанное относительно H условие максимума заменяется условием минимума H, то есть:

. (П.7.10)

Существенное преимущество принципа максимума по сравнению с классическим вариационным исчислением (метод Лагранжа) состоит в том, что он применим для любого множества U.

Задачи со свободным конечным временем. В ряде задач оптимального управления конечное время t₁ = T не задано, тогда говорят о задачах со свободным конечным временем.

Частным случаем таких задач является задача на быстродействие, когда надо минимизировать функционал

.

 

При этом f₀ º 1, тогда получим , т.е. минимизируем интервал управления.