 |
|
Общие свойства функции распределения
- Функция распределения F(x) есть неубывающая функция своего аргумента, т. е. при x2 >x1 , F(x2) > F(x1)
- На минус бесконечности функция распределения равна нулю:
F(- оо)= 0
- На плюс бесконечности функция распределения равна единице
F(+ оо)= 1
Очевидно, если рассматривать случайную величину Х как случайную точку Х на оси Ох, которая в результате опыта может занять то или иное положение, то функция распределения F(x) есть вероятность того, что случайная точка Х в результате опыта попадет левее точки х.
Будем увеличивать х, т. е. перемещать точку х вправо по оси абсцисс. Очевидно, при этом вероятность того, что случайная точка Хпопадет левее х, не может уменьшиться; следовательно, функция распределения F(x)с возрастанием хубывать не может. Докажите аналогичным способом второе и третье свойство функции распределения
График функции распределения F(x) в общем случае представляет собой график неубывающей функции (рисунок 1), значения которой начинаются от 0 и доходят до 1, причём в отдельных точках функция может иметь скачки (разрывы).
| х |
| F(x) |
| Рисунок 1 |
По мере увеличения числа значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки –меньше, ступенчатая кривая становится более плавной, случайная величина приближается к непрерывной величине, а её функция распределения – к непрерывной функции.
Функция f(x) –производная от функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения или дифференциальной функцией распределения (кривая распределения)
Зная распределения вероятностей, интересующих случайных величин, можно делать статистические выводы о событиях, в которых эти случайные величины участвуют, проверять гипотезы, оценивать параметры.
Но среди всех вероятностных распределений есть такие, которые используются на практике особенно часто. Среди дискретных распределений – это биноминальное и пуассоновское, среди непрерывных – показательное и нормальное.
Основные распределения и их генерация в Excel
Биноминальное распределение – одно из самых распространенных дискретных распределений, которое служит вероятностной моделью для многих явлений. Оно возникает в тех случаях, когда нас интересует сколько раз происходит некоторое событие в серии из определенного числа независимых событий (опытов).
Биномиальное распределение (распределение Бернулли) - распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна p
Пример
Для удобства и наглядности будем полагать, что нам известна величина p – вероятность того, что вошедший в магазин посетитель окажется покупателем и (1– p) = q – вероятность того, что вошедший в магазин посетитель не окажется покупателем.
Если X – число покупателей из общего числа n посетителей, то вероятность того, что среди n посетителей оказалось k покупателей равна
P(X= k) = 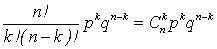 , (1)
, (1)
Формулу (1) называют формулой Бернулли
Если эту последовательность оборвать, то из последовательности независимых испытаний Бернулли получаются биномиальная, геометрическая, паскалева и отрицательная биномиальная случайные величины
Биномиальная случайная величина (m|n,p) – число m успехов в n испытаниях.
Свойства:
- Математическое ожидание MX = np
- Дисперсия DX= np(1-p)
- Биноминальное распределение может быть аппроксимировано нормальным распределением или распределением Пуассона.
Пакет анализа данных Excel содержит средства для генерации случайных чисел по некоторым известным распределениям. Пакет доступен через меню Сервис,команда- Анализ данных. Если данной команды нет в меню, необходимо выбрать из этого же меню команду «Надстройка». В появившемся окне выставить флажок (т.е. пометить) возле инструмента «Пакет анализа».С помощью процедуры «Генерация случайных чисел» данного пакета можно моделировать объекты, имеющие случайную природу, по заданному распределению вероятностей.
Для этого надо вызвать процедуру «Генерация случайных чисел» через команду Сервис, Анализ данных :
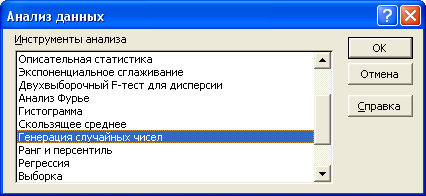
Рисунок 2 – Сервис, Анализ данных, Генерация данных
В следующем окне необходимо заполнить параметры: число переменных (определяет - сколько случайных величин моделируем); число случайных чисел (означает - сколько значений будет иметь одна случайная величина); вид распределения, его параметры и выходной интервал.
| Нажмите кнопку ОК, и получите выборки значений случайной величины |

Рисунок 3 - Генерация биноминального распределения
Распределение Пуассонаиграет важную роль в ряде вопросов физики, теории связи, теории надежности, теории массового обслуживания – словом, всюду, где в течение определенного времени может происходить случайное число каких-то событий (радиоактивных распадов, телефонных вызовов, отказов оборудования, несчастных случаев и т.п.)
Рассмотрим наиболее типичную ситуацию, в которой возникает распределение Пуассона. Пусть некоторые события могут происходить в случайные моменты времени, а нас интересует число появлений таких событий в промежутке времени от 0 до T (например, количество звонков, поступающих на АТС). Сделаем следующие предположения,:
- Вероятность появления события за малый интервал времени длины D примерно пропорциональна D, т.е. равна аD + о(D), где а>0 – параметр задачи, отражающий среднюю частоту событий
- Если в интервале времени длины D уже произошло одно событие, то условная вероятность появления в этом же интервале другого события стремится к нулю при D -> 0
- Количество событий, происшедших на непересекающихся интервалах времени, независимы как случайные величины.
В этих условиях случайное число событий, происшедшее за время от 0 до Т распределено по закону Пуассона с параметром 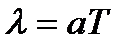
Свойства :
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона с параметром 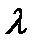 , равны параметру
, равны параметру 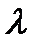
Связь с другими распределениями:
- При большом n и малом р существует связь между биноминальным распределением и распределением Пуассона.
- При 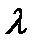 > 9, распределение Пуассона может быть аппроксимировано нормальным распределением со средним
> 9, распределение Пуассона может быть аппроксимировано нормальным распределением со средним 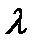 и дисперсией
и дисперсией 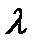
- Сумма m независимых случайных величин, имеющих пуассоновские распределения 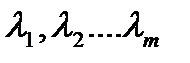 соответственно, имеет также распределение Пуассона с параметром
соответственно, имеет также распределение Пуассона с параметром 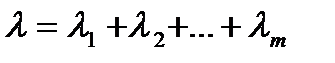
Для генерации чисел, распределенных по Пуассоновскому закону с помощью пакета анализа, после выполнения команды: Сервис, Анализ данных, Генерация случайных чиселнеобходимо указать вид распределения – пуассоновское, и значение параметра 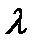 .
.
Показательное распределение играет базовую роль по крайней мере в двух областях применения статистических методов. К первой из них относятся задачи, связанные с данными типа «времени жизни». Понимать этот термин следует достаточно широко. В медико-биологических исследованиях под ним может подразумеваться продолжительность жизни больных при клинических исследованиях, в технике – продолжительность безотказной работы устройств, в психологии –время, затрачиваемое испытуемым на выполнение тестовых задач и т.д.
Второй областью активного использования показательного распределения являются задачи массового обслуживания. Здесь речь может идти об интервалах между обращениями клиентов, телефонными звонками и т.п. В пуассоновской модели интервалы времени между появлениями последовательных событий имеют показательное распределение.
Показательное распределение часто называют экспоненциальным. Параметр в некоторых областях именуют «отношением риска» В некоторых задачах вместо µиспользуют параметр b , b = 1/ µ
Свойства:
- Математическое ожидание: MX =1/ µ
- Дисперсия DX = 1/ µ 2
- Среди других распределений данное распределение выделяется отсутствием «памяти» (отсутствие последействия)
Связь с другими распределениями: Показательное распределение является частным случаем гамма распределения.