Главная | Обратная связь

Найпростіший потік викликів

Розподіл Пуассона

Стаціонарний ординарний потік без післядії називається найпростішим (пуассонівський, потоком чистої випадковості І роду). Задається найпростіший потік сімейством імовірностей надходження викликів в інтервалі часу t. Для визначення функції проведемо дослідження процесу надходження i викликів протягом двох сусідніх довільно розташованих на осі часу інтервалів t та Dt.

B інтервал [t+Δt] може потрапити і викликів в результаті однієї з таких незалежних подій:

· за інтервал t надійде і викликів, а за інтервал Δt – 0 викликів,

· або за інтервал t надійде (і-1) викликів, а за інтервал Δt – 1

· ...

· за інтервал t надійде 0 викликів, а за інтервал Δt – і викликів:

Тоді

, (2.9)

де – імовірність такої спільної події: в інтервалі часу tнадходить i-j викликів, а в інтервалі часу Δt надходитьjвикликів.

Оскільки спільно відбуваються дві незалежні події (через відсутність післядії імовірність надходження викликів в інтервалі часу Δt не залежить від числа викликів, що надійшли за часt), імовірність такої спільної події дорівнює добутку двох безумовних імовірностей і . Отже (2.9) приймає вид:

. (2.10)

Рівняння (2.10) можна значно спростити, якщо врахувати умову ординарності (2.3)

. (2.11)

Імовірність визначаємо з виразу (2.6) також з урахуванням ординарності потоку:

, (2.12)

а імовірність:

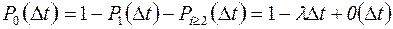. (2.13)

Підставимо вираз (2.12) і (2.13) у систему рівнянь (2.11), потім перенесемо в ліву частину рівнянь 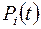та поділимо обидві частини рівнянь на :

P_i(t+Δt) = P_i(t)*(1-λ*Δt)+ P_i-1(t)* λ*Δt+O(Δt)

P_i(t+Δt) = P_i(t) - P_i(t) λ*Δt+ P_i-1(t)* λ*Δt+O(Δt)

P_i(t+Δt) - P_i(t) = - λ P_i(t) *Δt+ λ P_i-1(t)*Δt+O(Δt)

{P_i(t+Δt) - P_i(t)}/Δt = - λ P_i(t) + λ P_i-1(t)+O(Δt) Δt

Переходячи до границі при , одержуємо систему диференційних рівнянь:

. (2.14)

Початковими умовами для системи (2.14) є

. (2.15)

Розв’язанням (2.14) з урахуванням умов (2.15) є формула (розподіл) Пуассона:

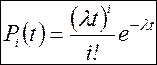. (2.16)

Цей вираз визначає імовірність надходження числа викликів i за час t.

Крім того, можна обчислити:

· імовірність P_o(t) відсутності викликів потоку за час t:

P_o(t) = e^-λt (2.17)

· імовірність наявності викликів потоку за час t:

P_³1 (t)= 1 - e^-λt (2.18)

· імовірність наявності не більше k викликів потоку за час t:

(2.19)

· імовірність наявності не менше k викликів потоку за час t:

= 1 - (2.20)

Приклад 2.1.

Виклики найпростішого потоку надходять в середньому через 2 хв.

Знайти : 1) імовірність надходження 2 викликів за 1 хв.

2) імовірність відсутності виклику за 2 хв.

3) імовірність надходження 3 викликів за 2 хв.

Рішення

Для того, щоб скористатися формулою Пуассона, потрібно знати параметр потоку l. Оскільки в найпростішому потоці параметр та інтенсивність співпадають і зворотно пропорційні середньому часу між віикликами, то:

l = 1/z = 0,5 викл/хв

1) lt = 0,5; P₂ = (0,5)²/2!*e^-0,5 = 0,0758

2) lt = 1; P₀ = e^-1 = 0,3679

3) lt = 1; P₃ = 1³/3!*e^-1 = 0,0613

Приклад 2.2.

Для найпростішого потоку з параметром 30 викл/год знайти імовірність надходження 2 викликів за 2 хв., та не більше 3 викликів за 5 хв.

Рішення

Спочатку узгодимо одиниці виміру параметру та часових інтервалів:

l = 30 викл/год = 0,5 викл/хв

1) lt = 0,5*2 = 1;

P₂ = 1²/2!*e^-1 = 0,18

2) lt = 2,5;

P_≤3 = P₀ + P₁ + P₂+ P₃ = e^-2,5 + 2,5* e^-2,5 +2,5²/2* e^-2,5 +2,5³/6* e^-2,5 = 0,76