 |
|
Аналіз розподілу Пуассона
Проаналізуємо розподіл Пуассона, тобто з’ясуємо коли значення імовірностей зростають, коли убувають, та які мають максимуми. Для чого розглянемо співвідношення двох послідовних членів: i-го та (i-1)-го.

Тут можливі 2 ситуації:
1) lt/i ³ 1, тобто приi £ lt ряд зростає: Pi (t) ³ Pi -1(t)
2) lt/i £ 1, тобто при i³ lt ряд убуває: Pi (t) £ Pi -1(t)
Таким чином, із зростанням iімовірністьPi (t)зростає,покиi < lt и починає убувати при i > lt. Розподіл Пуассона має наступні максимуми:
– 2 максимуми при lt цілому: i1 = lt, i2 = lt-1;
– 1 максимум при lt дробовому: i = [lt] (квадратними дужками позначено цілу частину від lt).
Побудуємо розподіл Пуассона для lt = 5. Розраховані за (2.16) значення імовірностей наведено в таблиці 2.1, графік – на рис. 2.2 а) На рис.2.2.б) і в) наведені аналогічні графіки для lt = 0,5 і lt = 3,5.
Таблиця 2.1
| i | ||||||||||
| Pi | 0,0067 | 0,034 | 0,084 | 0,1404 | 0,175 | 0,175 | 0,146 | 0,104 | 0,065 | 0,036 |


Рисунок 2.2. Графіки розподілу Пуассона для
а) lt = 5, б) lt = 0,5, в) lt = 3,5
Як видно з рисунка 2.2 а), при lt= 5 значення імовірностей зростають до і = 4, мають два максимуми і = 4 та і = 5, після чого починають убувати. У випадку, коли lt = 0,5, максимум розподілу Пуассона спостерігається для і=0, зростаюча частина графіку відсутня (бо і не може приймати значення менше 0). При lt = 3,5, максимум розподілу Пуассона спостерігається для і=3, значення імовірностей зростають до цього значення, після чого починають убувати.
Приклад 2.3
Визначити найбільш імовірне число викликів найпростішого потоку з параметром 120 викл/год за 180 с.
Рішення
lt = 120/60*3 = 6;
Pmax = P6 = P5
Дійсно:
P6 = 66/6!*e-6
P5 = 65/5!*e-6
Тобто, P5 = P6
Отже, найбільш імовірним є надходження 5 або 6 викликів такого потоку.
Важливою особливістю розподілу Пуассона є рівність математичного очікування та дисперсії випадкової величини, розподіленої за цим законом.
За визначенням, математичне очікування Мх дискретної випадкової величини Х, що має відомий закон розподілу p(x):
Мх = М[X]= 
Для нашого випадку випадкова величина і (кількість викликів, що потрапила до інтервалу заданої довжини), розподілена за законом Пуассона з імовірностями, що визначаються (2.16). Тоді
Mi =  =
= 
 =
=
= (λt)*  *
* 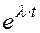 = λt
= λt
Аналогічно
Dі =  - (Mi)2 =
- (Mi)2 = 
 (λt)i/i! – (λt)2 = λt
(λt)i/i! – (λt)2 = λt
Таким чином,
Mі = Dі = lt
Ця властивість використовується на практиці для обгрунтованого висунення гіпотези, чи можна рахувати заданий потік найпростішим. Перевірку цієї статистичної гіпотези здійснюють з використанням відповідних статистичних критеріїв, наприклад – критерію Пірсона [5].