Главная | Обратная связь

Перевірка відповідності реального потоку моделі найпростішого

Досить часто при дослідженні процесів, що відбуваються в телекомунікаційних системах, в наявності є статистична інформація, отримана в ході спостереження за реальними вхідними та вихідними потоками. Для використання отриманих вище формул треба впевнитися, що ці потоки можна вважати найпростішими.

Для перевірки даних, отриманих статистичним шляхом, використовують різні статистичні критерії, наприклад критерій Пірсона [2].

2 підходи, залежно від того, які вимірювання здійснювались для реального потоку.

 

І спосіб.

Якщо підраховувалась кількість викликів, що потрапили до послідовності часових інтервалів заданої довжини, то перевіряється їх відповідність розподілу Пуассона. Найпростішою ознакою такого розподілу є рівність точечних оцінок математичного очікування та дисперсії, тобто вібіркового середнього та віправленої дисперсії.

Таким чином, якщо з деякої генеральної сукупности Х(t) – значень кількості викликів, що потрапили до послідовності часових інтервалів заданої довжини, зроблено вибірку та виконано її статистичну обробку, то можна отримати таблицю статистичного розподілу дискретної випадкової величини у вигляді таблиці 2.2.

Таблиця 2.2

Статистичний розподіл кількості викликів потоку, що потрапили у заданий інтервал

X (t)і	X (t)1	X (t)2	…	X (t)k
nі	n1	n2	…	nk

де X(t)_і – кількість викликів, що попали у n_і інтервалів (загальна кількість інтервалів ).

Після чого обчислюються статистичні оцінки математичного очікування та дисперсії числа викликів, що потрапили до кожного інтервалу:

Вибіркове середнє:

M_x = 1/N *n_i

Виправлена дисперсія:

D_x = 1/(N-1)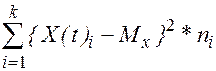

При M_x ≈ D_x доцільно висувати і перевіряти гіпотезу , що потік є найпростішим. Перевірка гіпотези здійснюється за відомими статистичними критеріями, наприклад критерієм Пірсона (додаток 1).

 

ІІ спосіб.

Якщо вимірювались інтервали часу між двома послідовними викликами, то перевіряється їх відповідність експоненціальному розподілу, тобто рівність математичного очікування та середньоквадратичного відхилення (СКВ). Таким чином, якщо задана таблиця статистичного розподілу випадкової величини у вигляді таблиці 2.3,

Таблиця 2.3

Статистичний розподіл інтервалу між послідовними викликами потоку

zі	z1	z2	…	zk
nі	n1	n2	…	nk

де z_і – значення часу між послідовними викликами, n_і – кількість таких значень (загальна кількість вимірів ), то обчислюються вібіркове середнє та виправлене СКВ:

 

M_z = 1/N *n_i

D_z = 1/(N-1)

σ_z =

 

При M_z ≈ σ_z можна висувати і перевіряти гіпотезу , що потік є найпростішим.

 

Приклад 2.4.

В результаті статистичної обробки інтервалів часу між викликами в потоці тримані наступні характеристики: середнє значення інтервалу: m_z=2 c; дисперсія D_z=4,03 c. Визначити імовірність відсутності викликів за 1 с. Обґрунтувати відповідь.

 

 

Рішення

Оскільки вимірювались інтервали часу між викликами в потоці, користуємось другим способом перевірки і обчислимо σ_z = = 2 с. Тобто, M_z ≈ σ_z і потік можна вважати найпростішим. Відповідно, імовірність відсутності викликів за 1 с можна вирахувати за формулою Пуассона, а саме (2.17). Параметр потоку визначаємо як величину, зворотну середньому інтервалу між викликами:

λ = 1/z = ½ = 0.5 викл/с

P_o(t) = = e^-0.5*1 = 0.6