 |
|
Марківський ланцюг з дискретним часом
Випадковий процес, що відбувається в системі S, називається марківським (процесом без післядії) , якщо для деякого моменту часу t0 імовірність будь-якого стану в майбутньому (t0 >0) залежить тільки від її теперішнього стану (t0 =0) і не залежить від того, коли і як система попала в цей стан (тобто від попередніх подій).
Випадковий процес називається марківським ланцюгом (процесом з дискретними станами), якщо всі можливі стани системи можна перелічити S1 , S2, S3 ..., а сам процес полягає в тому, що час від часу система миттєво (стрибком) переходить з одного стану в інший.
Тоді процес можна подати у вигляді графу станів:
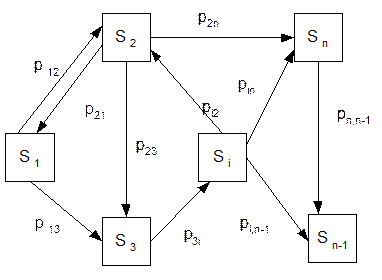
Рисунок 4.1. Граф станів
Якщо переходи системи з Sі в Sj можливі тільки в чітко визначені, заздалегідь фіксовані моменти t1, t2, ...маємо марківський ланцюг з дискретним часом.
Розглянемо марківський ланцюг з дискретним часом як функцію цілочисельного аргументу 1, 2, ... k (номер крока). Позначимо Si(k) – після k кроків система знаходиться в стані Si. Звичайно, для будь-якого k система має знаходитися в одному з можливих станів, тобто події S1(k), S2(k), S3(k), ..., Si(k), ... , Sn(k) утворюють повну групу подій.
Позначимо pij(k) – імовірність того, що на k кроці система перейде із стану Si в стан Sj. Оскільки ми розглядаємо марківський ланцюг, то для будь-якого кроку перехідна імовірність pij(k) не залежить від попередніх подій, тобто через які стани система попала в стан Si .
Якщо перехідна імовірністьpij(k) не залежить також від номеру кроку k , тобто pij(k) = pij = const, то маємо однорідний марківський ланцюг, інакше – неоднорідний.
Розглянемо однорідний марківський ланцюг, заданий матрицею переходу:
p11 p12 … p1j … p1n
p21 p22 … p2j … p2n
[pij] = … … … … … … (4.1)
pi1 pi2 … pij … pin
… … … … … …
pn1 pn2 … pnj … pnn
pij – імовірність того, що за 1 крок система перейде із стану Si в стан Sj. Фактично, це – умовна імовірність того, що на k кроці система опиниться в стані Sj при умові, що на (k-1) кроці вона була в стані Si.
pij = P (Sj(k)/Si(k-1))
piі - імовірність того, що за 1 крок система залишиться в стані Si
Деякі з елементів матриці можуть дорівнювати нулю. Це означає, що відповідні переходи неможливі (якщо pij = 0, за 1 крок система не може перейти із стану Si в стан Sj).
Для кожного рядка матриці переходу сума всіх імовірностей повинна дорівнювати 1 (оскільки на кожному кроці система має або перейти в якийсь стан, або залишитися в початковому):
 для i = 1, n (4.2)
для i = 1, n (4.2)
Рівняння (4.2) називається умовою нормування.
Поставимо задачу:
знайти Pi(k) – імовірності будь-якого і-го стану системи після k-го кроку.
Якщо в початковий момент система знаходиться у стані Sm , то імовірність цього стану на нульовому кроці дорівнює 1, а всіх інших – 0:
P1(0) = 0, P2(0) = 0, …, Pn(0) = 0, Pm(0) = 1
За перший шаг система може перейти в один із станів S1, S2, …, Sn з імовірностями, заданими відповідним (m-м) рядком матриці переходу:
S1 S2 … Sm … Sn
pm1 pm2 … pmm … pmn
Отже, імовірності після першого кроку марківського ланцюга:
P1(1) = pm1, P2(1) = pm2, …, Pn(1) = pmn, Pm(1) = pmm (4.3)
Обчислення імовірностей на наступному кроці є більш складною задачею, оскільки нам невідомий точний стан системи на першому кроці, а є тільки припущення щодо цього і відповідні імовірності можливих станів системи (4.3). Скористаємося формулою повної імовірності [5]: якщо деяка подія А може відбутися тільки сумісно з якимись подіями (гіпотезами) Н1, Н2, …, Нn, що утворюють повну групу подій, то

В нашому випадку умовні імовірності дає матриця переходу (4.1), а гіпотезами виступають припущення, що система на першому кроці була в тому або іншому стані, ці імовірності дає рівняння (4.3).
Таким чином для обчислення імовірності того, що система на другому кроці буде, наприклад, в стані S1, ми маємо розглянути всі можливікомбінації. Система на попередньому (першому) кроці могла бути в першому стані з імовірністю P1(1) і за другий крок не здійснити ніяких переходів, тобто лишитися в цьому ж стані з імовірністю p11, або бути в другому стані з імовірністю P2(1) і за другий крок перейти в перший з імовірністю p21 і т.д.:
P1(2) = P1(1)*p11 + P2(1)*p21 + ... + Pn(1)*pn1 = 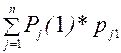
Для стану Sі
Pі(2) =  , і = 1,…,n
, і = 1,…,n
Для 3 кроку усі імовірності обчислюються через розраховані на другому кроці:
Pі(3) =  , і = 1,…,n
, і = 1,…,n
Для k-го кроку використовується рекурентна формула через (k-1)-й крок:
Pі(k) =  , і = 1,…,n (4.4)
, і = 1,…,n (4.4)
Приклад 4.1.
По мішені здійснюється 4 постріли у фіксовані моменти часу t1, t2, t3, t4..
Можливі наступні стани мішені:
S1 – мішень не ушкоджено, S2 - мішень незначно ушкоджено
S3 - мішень значно ушкоджено, S4 – мішень зруйновано
Імовірності переходу між станами за 1 крок задано розміченим графом:

Рисунок 4.2.
В початковий момент часу мішень неушкоджена (S1). Визначити імовірності станів після 4 пострілів.
Рішення.
За графом станів заповнимо матрицю перехідних імовірностей.
0,3 0,4 0,2 0,1
0 0,4 0,4 0,2
[pij] 0 0 0,3 0,7
0 0 0 1
В початковий момент система знаходиться у стані S1 , тобто P1(0) = 1
Тому імовірності системи після першого пострілу (першого кроку марківського ланцюга) дає перший рядок матриці переходу:
P1(1)= 0,3 P2(1)= 0,4 P3(1)= 0,2 P4(1)= 0,1
Для обчислення імовірностей системи після другого кроку розглядаємо всі можливі випадки за формулою (4.4):
P1(2) = P1(1)*p11 + P2(1)*p21 + P3(1)*p31 + P4(1)*p41 =
= 0,3*0,3 = 0,09
P2(2) = P1(1)*p12 + P2(1)*p22 + P3(1)*p32 + P4(1)*p42 =
= 0,3*0,4 + 0,4*0,4 = 0,28
P3(2) = P1(1)*p13 + P2(1)*p23 + P3(1)*p33 + P4(1)*p43 =
= 0,3*0,2 +0,4*0,4 +0,2*0,3 = 0,28
P4(2) = P1(1)*p14 + P2(1)*p24 + P3(1)*p34 + P4(1)*p44 =
= 0,3*0,1 + 0,4*0,2 + 0,2*0,7 + 0,1*1 = 0,35
Перевірка:
0,09+0,28+0,28+0,35 = 1
Третій крок:
P1(3) = P1(2)*p11 + P2(2)*p21 + P3(2)*p31 + P4(2)*p41 =
= 0,09*0,3 = 0,027
P2(3) = P1(2)*p12 + P2(2)*p22 + P3(2)*p32 + P4(2)*p42 =
= 0,09*0,4 +0,28*0,4 = 0,148
Аналогічно
P3(3) = 0,214
P4(3) = 0,611
0,027 + 0,148 + 0,214 + 0,611 = 1
Для 4 кроку використовуємо імовірності станів, обчислені на третьому кроці:
P1(4) = 0,0081
P2(4) = 0,0700
P3(4) = 0,1288
P4(4) = 0,7931
0,0081 +0,0700 + 0,1288 + 0,7931 = 1
Розглянемо більш загальний випадок – неоднорідного марківського ланцюга, для якого перехідні імовірності змінюються, тобто матриця переходу задана у вигляді [pij(k)], де pij(k) = P(Sj(k)/Si(k-1)). В цьому випадку рівняння (4.3) матиме вигляд:
Pі(k) =  , і = 1,…,n
, і = 1,…,n