Потік з обмеженою післядією

В потоці з обмеженою післядією імовірність надходження нового виклику в інтервалі τ залежить тільки від розташування цього інтервалу відносно моменту надходження останнього виклику і не залежить від часу надходження решти викликів. Для таких потоків в момент надходження виклику майбутнє не залежить від минулого й уся післядія обмежується величиною інтервалу між викликами.

Особливе місце серед потоків з обмеженою післядією занімають рекурентні потоки, для яких усі інтервали між викликами, враховуючи перший, мають однаковий розподіл F_k(t) = F(t) при k ³ 1, і рекурентні потокиіз запізненням, в яких тільки першийінтервал має розподіл, відмінний від інших. Рекурентні потокиіз запізненням задаються відповідно двома функціями розподілу: F₁(t) і F_k(t) = F(t) при k ³ 2. Функція F₁(t) характеризує розподіл інтервалу часу від довільно обраного початку відліку t₀ до моменту надходження першого виклику.

Можна показати, що стаціонарний рекурентний потік буде найпростішим. Стаціонарний рекурентний потік із запізненням називають потоком Пальма. Потік Пальма задається умовною імовірністю j₀(t) відсутності викликів в інтервалі довжиною t, якщо в початковий момент цього інтервалу надійшов виклик. Тоді

(2.44)

Тут λ – параметр або інтенсивність потоку Пальма, 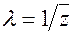. Потік Пальма є узагальненням найпростішого потоку. При маємо найпростіший потік, оскільки усі інтервали, враховуючи перший, розподілені за експоненціальним законом. Модель потоку Пальма добре описує потік викликів, які не отримали обслуговування в комутаційній системі (втрачених). Має місце наступна теорема Пальма.

Якщо на комутаційну систему з явними втратами надходить потік викликів типу Пальма і час обслуговування розподілений за експоненціальним законом, то потік викликів, які не отримали обслуговування, також є потоком Пальма.

Зокрема, якщо вхідний потік є найпростішим, потік втрачених викликів має обмежену післядію і за своїми властивостями є потоком Пальма. Модель потоку Пальма використовується для розрахунку неповнодоступних включень. Певну складність при цьому додає та обставина, що при об’єднанні двох і більше незалежних потоків Пальма сумарний потік за своїми властивостями буде відрізнятися від потоку Пальма. Але при роз’єднанні потоку Пальма на декілька напрямків, так що з імовірністю Р_і виклик надходить на і-й напрямок, потік і-го напрямку також буде потоком Пальма.

Поняття „потік Пальма” об’єднує широкий клас потоків, що відрізняються один від одного законом розподілу інтервалу між викликами. Одним з прикладів потоку Пальма є потік Ерланга, який отримується просіюванням найпростішого потоку. Якщо з останнього викинути кожний другий виклик, решта утворить потік Ерланга другого порядку. Якщо в найпростішому потоці зберегти кожний третій виклик, матимемо потік Ерланга третього порядку. Таким чином, потоком Ерланга п-ого порядку називається потік, отриманий з найпростішого потоку збереженням кожного п-ого виклику та відкиданням решти. Звичайно, найпростіший потік можна розглядати як потік Ерланга першого порядку.

Інтервали між викликами в потоці Ерланга незалежні між собою та однаково розподілені, оскільки вони є сумою однакового числа незалежних інтервалів найпростішого потоку. Найдемо закон розподілу інтервалу z(n) між викликами в потоці Ерланга п-ого порядку. Між (k-1)-мі k-мвикликами потоку Ерланга були п-1 відкинуті виклики початкового найпростішого потоку. Щільність імовірності величини z(n) позначимо p_n(t). Це означає, що з імовірністю p_n(t)Dt величина z(n) прийме значення, що знаходиться в діапазоні між t і t+Dt. Для цього необхідно, щоб одночасно відбулися дві події: в інтервал [t,t+Dt) потрапив k-йвиклик (імовірність такої події дорівнює λDt), а в інтервал довжиною t потрапив п-1 виклик початкового найпростішого потоку (цю імовірність обчисюємо за формулою Пуассона). За теоремою добутку імовірностей отримуємо:

Скоротивши на Dt, можна отримати закон розподілу Ерланга п-ого порядку:

(2.45)

При п=1 (2.45) дає експоненціальний розподіл (2.22).

Математичне очікування і дисперсію величини z(n) зручно визначити відповідно до теореми суми математичних очікувань і дисперсій незалежних випадкових величин [5], тобто інтервалів між викликами початкового найпростішого потоку:

Параметр потоку Ерланга п-ого порядку:

Відповідно до (2.44) визначимо закон розподілу першого інтервалу потоку:

Для розглянутого потоку із зростанням n характерне збільшення математичного очікування і дисперсії інтервалу z(n) і відповідне зменшення параметру. Змінимо масштаб часу так, щоб математичне очікування інтервалу z(n) і параметр потоку Λ_п залишалися незмінними, незалежними від n. Для цього введемо нормований інтервал . Потік з такими інтервалами між викликами назвемо нормованим потоком Ерланга п-ого порядку (рис. 2.4 б). Приведемо інтегральну функцію та щільність розподілу інтервалу z_н(n), а також його математичне очікування і дисперсію:

Із збільшенням n дисперсія необмежено убуває і нормований потік Ерланга наближується до детермінованого з постійними інтервалами, рівними .

Таким чином, використовуючи модель нормованого потоку Ерланга при різних значеннях n, можна отримати будь-яку ступінь випадковості: від потоку чистої випадковості (найпростіший потік) до детермінованого. Однак при цьому завжди зберігається жорсткий функціональний зв’язок між математичним очікуванням і дисперсією інтервалу між викликами: . Це ускладнює заміну потоком Ерланга реального потоку з довільним співвідношенням Mz i Dz.

Узагальнимо розглянуту модель потоку. Припустимо, що інтервал між викликами z(n) є сума n випадкових величин, кожна з яких розподілена за експоненціальним законом із своїм параметром . Такий потік називається узагальненим потоком Ерланга п-ого порядку (рис. 2.4 в). Його функція та щільність розподілу, а також математичне очікування і дисперсія мають вигляд:

(2.46)

Використання узагальнених потоків Ерланга дещо розширює можливості з апроксимації реальних потоків з обмеженою післядією, але і в цьому випадку зберігається співвідношення .

Від цього обмеження вільна модель потоку з інтервалами, розподіленими за комбінованим експоненціальним законом (рис. 2.4 г). Нехай інтервал z(n) складається з випадкового числа фаз, кожна з яких розподілена за експоненціальним законом з параметром . Після k-ої фази з імовірністю q_k надходить виклик, а з імовірністю p_k = 1 – q_k настає наступна (k+1)-а фаза. Максимально можливе число фаз дорівнює n (q_п = 1, p_п = 0). Функція та щільність розподілу інтервалу z(n), а також його математичне очікування і дисперсія представлені у формулах (2.47) та (2.48) відповідно.

(2.47)

(2.48)

В окремому випадку при n=2 . Нескладно перевірити, що при має місце , а при – зворотнє співвідношення. Змінюючи параметри q_r , p_r і λ_r , можна підібрати потік з будь-якими заданними значеннями довільного числа моментів величини z(n). Зокрема, при з розподілу (2.47) отримуємо (2.46).

Наступною моделлю потоку Пальма, що широко використовується для апроксимації реальних потоків, є переривчастий пуассонівський потік п-ого порядку. Інтервали між викликами в даному потоці розподілені за гіперекспоненціальним розподілом (рис. 2.4 д):

(2.49)

Розподіл (2.49) має наступну інтерпретацію: з імовірністю q₁ інтервал між викликами розподілено за експоненціальним розподілом з параметром λ₁, з імовірністю q₂ – за експоненціальним розподілом з параметром λ₂ і т.д.

При λ_і = λ даний розподіл переходить в експоненціальний, а при – в узагальнений розподіл Ерланга п-ого порядку (2.46).

Розглянутий потік може бути утворений при пропусканні найпростішого потоку з параметром Λ через ключ. Якщо довжини інтервалів ввімкнення та вимкнення ключа розподілені за експоненціальним законом з параметрами a і b відповідно, то на виході ключа отримаємо переривчастий пуассонівський потік 2-ого порядку, характеристики якого можна вихначити наступним чином:

Потік 3-го порядку можна отримати, якщо на вхід подібного ключа буде надходити переривчастий потік 2-ого порядку. Взагалі при пропусканні через ключ потоку п-ого порядку на виході отримаємо потік (п+1)-ого порядку.

По аналогії з гіперекспоненціальним розподілом можна ввести гіперерлангівський розподіл п-ого порядку (рис 2.4 е).Він має наступну інтерпретацію: з імовірністю q₁ інтервал між викликами розподілено узагальненим розподілом Ерланга 1-ого порядку (експоненціальним розподілом), з імовірністю q₂ – за узагальненим розподілом Ерланга 2-ого порядку і т.д. Тоді

Гіперерлангівський розподіл п-ого порядку відповідає гіпер-експоненціальному т-ого порядку, де . Параметри гіперекспоненціального розподілу можна виразити через параметри гіперерлангівського наступним чином:

.

Гіперерлангівський розподіл в свою чергу можна розглядати як безпосереднє узагальнення комбінованого експоненціального. Замінивши параметри гіперерлангівського розподілу відповідно до приведених нижче формул, отримаємо комбінований експоненціальний розподіл з параметрами :

Можливий і зворотній перерахунок параметрів від комбінованого експоненціального до гіперерлангівського розподілу:

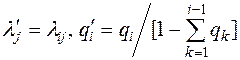
Але в цьому випадку загальне число різних параметрів λ у гіперерлангівського розподілу скоротиться до п.

Розглянуті розподіли надають широкі можливості для апроксимації реальних потоків. Використовуючи фізичну інтерпретацію, можна підібрати необхідний розподіл інтервалу z і визначити необхідні параметри через порівняння статистичних і теоретичних моментів (математичного очікування, дисперсії, асиметрії тощо). Але перед цим необхідно впевнитися, що розглянутий потік дійсно належить до класу потоків Пальма.

2.11 Контрольні питання

1. Навести властивості найпростішого потоку

2. Що означає стаціонарність, ординарність, післядія?

3. Які потоки можна вважати стаціонарними?

4. Які потоки мають післядію?

5. Навести числові характеристики найпростішого потоку

6. Дати визначення і пояснити різницю між параметром та інтенсивністю потоку. Для яких потоків ці характеристики співпадають і для яких – ні.

7. Навести формулу закону Пуассона

8. Навести властивості розподілу Пуассона.

9. За яким законом розподілено інтервали між викликами в найпростішому потоці?

10. За яким законом в найпростішому потоці розподілено число викликів, що потрапили в інтервали рівної довжини?

11. Як перевірити відповідність реального потоку моделі найпростішого, якщо виміряли інтервали між сусідніми викликами?

12. Як перевірити відповідність реального потоку моделі найпростішого, якщо для послідовності інтервалів рівної довжини підраховано число викликів, що потрапили в ці інтервали?

13. Який потік утворюється при об’єднанні найпростіших потоків?

14. До якого класу відноситься потік звільнень і чому?

15. Основна властивість експоненціального закону розподілу.

16. Чому дорівнює кількість джерел викликів в найпростішому потоці. Якою його властивістю це пояснюється?

17. Чи є примітивний потік стаціонарним? Ординарним?

18. Має примітивний потік післядію чи ні?

19. Чи є потік звільнень стаціонарним? Ординарним? У якому випадку?

20. Має потік звільнень післядію чи ні? У якому випадку?

21. Чи є потік з повторними викликами стаціонарним? Ординарним?

22. Має потік з повторними викликами післядію чи ні?

23. В якому випадку можна вважати примітивний потік найпростішим? Чому?

24. Поясніть сутність методу Монте-Карло.

25. Що таке потоки з обмеженою післядією та рекурентні потоки?

26. Дайте визначення потоку Пальма. Як він задається? В якому випадку можна вважати потік Пальма найпростішим? Чому?

27. Сформулюйте теорему Пальма. Як вона використовується при розрахунку комутаційних систем?

28. Який потік утворюється при об’єднанні потоків Пальма? Який потік утворюється при роз’єднанні потоку Пальма на декілька напрямків?

29. Дайте визначення потоку Ерланга. Як він утворюється?

30. Що таке нормований потік Ерланга? Який зв’язок існує між математичним очікуванням і дисперсією інтервалу між викликами в такому потоці?

31. Як можна отримати узагальнений потік Ерланга?

32. До якого класу потоків відноситься переривчастий пуассонівський потік п-ого порядку? За яким законом розподілено інтервал між викликами викликами в такому потоці?

2.12 Завдання для самостійної роботи

33. Для найпростішого потоку, в якому виклики надходять в середньому через 15 с, визначити найбільш імовірну кількість викликів за 5 хв.

34. При якому параметрі найпростішого потоку найбільш імовірним є надходження за 2 хв. 7 и 8 викликів?

35. На СМО надходить найпростіший потік викликів з інтенсивністю 12 викл/год. Найти імовірність того, що: за 2 хв. надійде хоча б 1 виклик.

36. Для деякого потоку отримані такі значення кількості викликів, що потрапили в 20 двохвилинних інтервалів: 5, 1, 1, 2, 4, 5, 4, 1, 6, 3, 6, 0, 5, 5, 4, 6, 2, 5, 2, 4. Чи можна вважати цей потік найпростішим? Визначити параметр потоку.

37. В результаті статистичної обробки інтервалів часу між викликами в потоці отримані такі характеристики: середнє значення інтервалу: m_z=5 c; дисперсія D_z=25,13 c. Визначити імовірність відсутності викликів за 1 с.

38. Система обслуговує 30 джерел викликів середньою інтенсивністю 3 викл/хв кожний. Визначити середнє, максимальне и мінімальне значення параметра потоку, якщо обслуговування виклику триває в середньому 5 с.

39. Визначити середнє значення параметра потоку, створеного групою з 40 джерел, якщо 1 джерело у вільному стані надсилає на обслуговування, в середньому, 6 викл/хв, а обслуговування 1 виклику триває, в середньому, 5 с.

40. Деяка система працює так, що кожний з 20 каналів одразу займається новим викликом після завершення обслуговування попереднього. Середній час обслуговування 600 с (експоненціальний закон). Визначити імовірність того, що за 1 хв. не звільниться жоден канал.

41. Потік генерується групою з 600 джерел, кожне з котрих потребує обслуговування, в середньому 1 раз в 2 години. Визначити імовірність наявності викликів за 20 с. Обґрунтувати допущення.

42. В початковий момент часу у з’єднувальній лінії є 5 викликів. Нехай тривалість розмови розподілена за експоненціальним законом із середнім значенням 3 хвилини. Обчислити імовірність, що рівно2 з тих 5 викликів ще будуть тривати через 1 хвилину.