 |
|
Поведение функции, стоящей под знаком сходящегося
Интеграла, на бесконечности.
Замечание:Убывание подынтегральной функции ее стремление к нулю не является необходимым условием сходимости интеграла на бесконечности.
Пример. 1°. Рассмотрим 
.
Особые точки: 
.
а). x = 0. 
– интеграл сходится "l по признаку сравнения.
b). x = +¥. Сходится, вообще говоря (в.г.), условно по признаку Дирихле ибо 
– монотонно стремится к нулю, а функция 
имеет ограниченную первообразную.
c). x = 1. Тоже применим мажорантный признак: 
, т.е. сходится абсолютно при 
. Таким образом, исходный интеграл сходится в.г. условно для .
Строго монотонная замена 
приводит к выводу о том, что 
также сходится условно при , хотя его подынтегральная функция 
для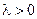 
неограниченна.
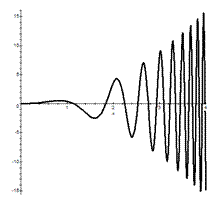
Происходит это за счет взаимного погашения площадей (см.Рис.).
Чтобы не создавалось впечатление, что сходимость появляется только за счет взаимного погашения площадей, приведем другой пример.
2°.Построим функцию 
, которая равна нулю при всех положительных значениях аргумента, кроме промежутков 
, где она равна единице.
Тогда, интеграл есть площадь и 
. Таким образом, неотрицательная функция на бесконечности не стремится к нулю и, тем не менее, интеграл от нее сходится.
Можно на этой идее построить и f (x) которая будет неограниченной, а интеграл будет сходиться.
Таким образом, сходимость 
не означает, что f (x) ® 0 при x ® ¥.
Но...
Т°. Если 
существует и конечен, то в случае сходимости интеграла на бесконечности
этот предел необходимо равен нулю.
Более того, если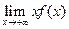 
существует и конечен, то он также равен нулю.
Интегралы Фрулани.
Пусть функция 
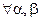таких, что 
и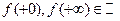 
.
Рассмотрим интеграл: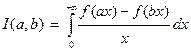 
. Интегралы такого типа называются интегралами Фрулани. Для них:
= 
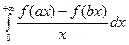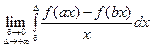. Тогда:
= 
= 
= 
=
= 
= 
= 
.
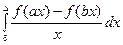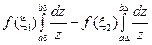И, следовательно = =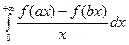 
.
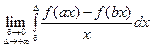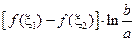Выполняя предельный переход при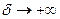 
и 
получаем:
.
Примеры:
1) 
.
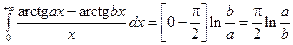2) 