 |
|
Деякі теореми про функції, що диференціюються
ЗМІСТОВИЙ МОДУЛЬ 7
ДОСЛІДЖЕННЯ ФУНКЦІЙ З ДОПОМОГОЮ ПОХІДНИХ
Тема 7.1. Дослідження функцій за допомогою похідних.
7.1.1. Деякі теореми про диференційовані функції.
7.1.2. Правило Лопіталя.
7.1.3. Зростання і спадання функцій.
7.1.4. Максимум і мінімум функцій.
7.1.5. Найбільше і найменше значення функції на відрізку.
7.1.6. Опуклість графіка функції. Точки перегину.
7.1.7. Асимптоти графіка функції.
7.1.8. Загальна схема дослідження функції і побудови графіка.
Тема 7.2. Формули Тейлора.
7.2.1. Формула Тейлора для многочленна.
7.2.3. Формула Тейлора для довільної функції.
Тема 7.3. Означення і представлення комплексних чисел.
7.3.1. Основні поняття.
7.3.2. Геометричне зображення комплексних чисел.
7.3.3. Формули запису комплексних чисел.
Тема 7.4. Дії над комплексними числами.
7.4.1. Додавання комплексних чисел.
7.4.2. Віднімання комплексних чисел.
7.4.3. Множення комплексних чисел.
7.4.4. Ділення комплексних чисел.
7.4.5. Добування кореня з комплексного числа.
ДОСЛІДЖЕННЯ ФУНКЦІЇ ЗА ДОПОМОГОЮ ПОХІДНИХ
Деякі теореми про функції, що диференціюються
Розглянемо ряд теорем, що мають велике теоретичне і прикладне значення.
Теорема 7.1.1 (Ролль). Якщо функція неперервна на відрізку, що диференціюється на інтервалі і на кінцях відрізка приймає однакові значення, то знайдеться хоча б одна точка, в якій похідна звертається в нуль, тобто .
□Оскільки функція неперервна на відрізку, то не досягає на цьому відрізку найбільшого і найменшого значень, відповідно, М і т. Якщо М=т, то функція  постійна на
постійна на  і, отже, її похідна
і, отже, її похідна  в будь-якій точці відрізка
в будь-якій точці відрізка  .
.

Рис.140. Рис. 141. Рис.139
Якщо  , то функція досягає хоча б одного із значень М абот у внутрішній точці з інтервалу, оскільки .
, то функція досягає хоча б одного із значень М абот у внутрішній точці з інтервалу, оскільки .
Нехай, наприклад, функція приймає значення М в точці, тобто  . Тоді для всіх
. Тоді для всіх  виконується співвідношення
виконується співвідношення

Знайдемо похідну в точці х=с:
 .
.
Через умову (7.1.1) вірно нерівність . Якщо (тобто праворуч від точки х=с), то
 і тому .
і тому .
Якщо то
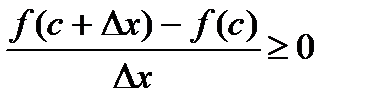 і .
і .
Таким чином .
У випадку, доказ аналогічний.■
Геометрична теорема Ролля означає, що на графіку функції  знайдеться точка, в якій дотична до графіка паралель осі Ох (див. Рис. 139 і 140). На малюнку 141 таких крапок дві.
знайдеться точка, в якій дотична до графіка паралель осі Ох (див. Рис. 139 і 140). На малюнку 141 таких крапок дві.
Теорема 7.1.2 (Коші). Якщо функції і безперервні на відрізку, що диференціюється на інтервалі, причому для, то знайдеться хоча б одна точка така, що виконується рівність
Відзначимо що 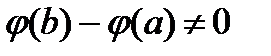 , оскільки в осоружному випадку по теоремі Ролля знайшлася б точка с, така, що
, оскільки в осоружному випадку по теоремі Ролля знайшлася б точка с, така, що  , чого не може бути по умові теореми. розглянемо допоміжну функцію
, чого не може бути по умові теореми. розглянемо допоміжну функцію
 .
.
Вона задовольняє все умовам теореми Ролля: неперервна на відрізку  і що диференціюється на інтервалі
і що диференціюється на інтервалі  , оскільки є лінійною комбінацією функцій і ; на кінцях відрізка вона приймає однакові значення .
, оскільки є лінійною комбінацією функцій і ; на кінцях відрізка вона приймає однакові значення .
На підставі теореми Ролля знайдеться точка  така що . Але
така що . Але  , отже
, отже
 .
.
Звідси слідує
 і .
і .
Теорема 7.1.3 (Лагранж). Якщо функції безперервні на відрізку, то знайдеться хоча б одна точка така, що виконується рівність
 .
.
□ Теорему Лагранжа можна розглядати як окремий випадок теореми Коші. Дійсно, поклавши  , знаходимо .
, знаходимо .
 Підставляючи ці значення у формулу
Підставляючи ці значення у формулу  , одержуємо або
, одержуємо або  .
.
Отриману формулу називають формулою Лагранжа абоформулою про кінцевий приріст: приріст функції, що диференціюється, на відрізку
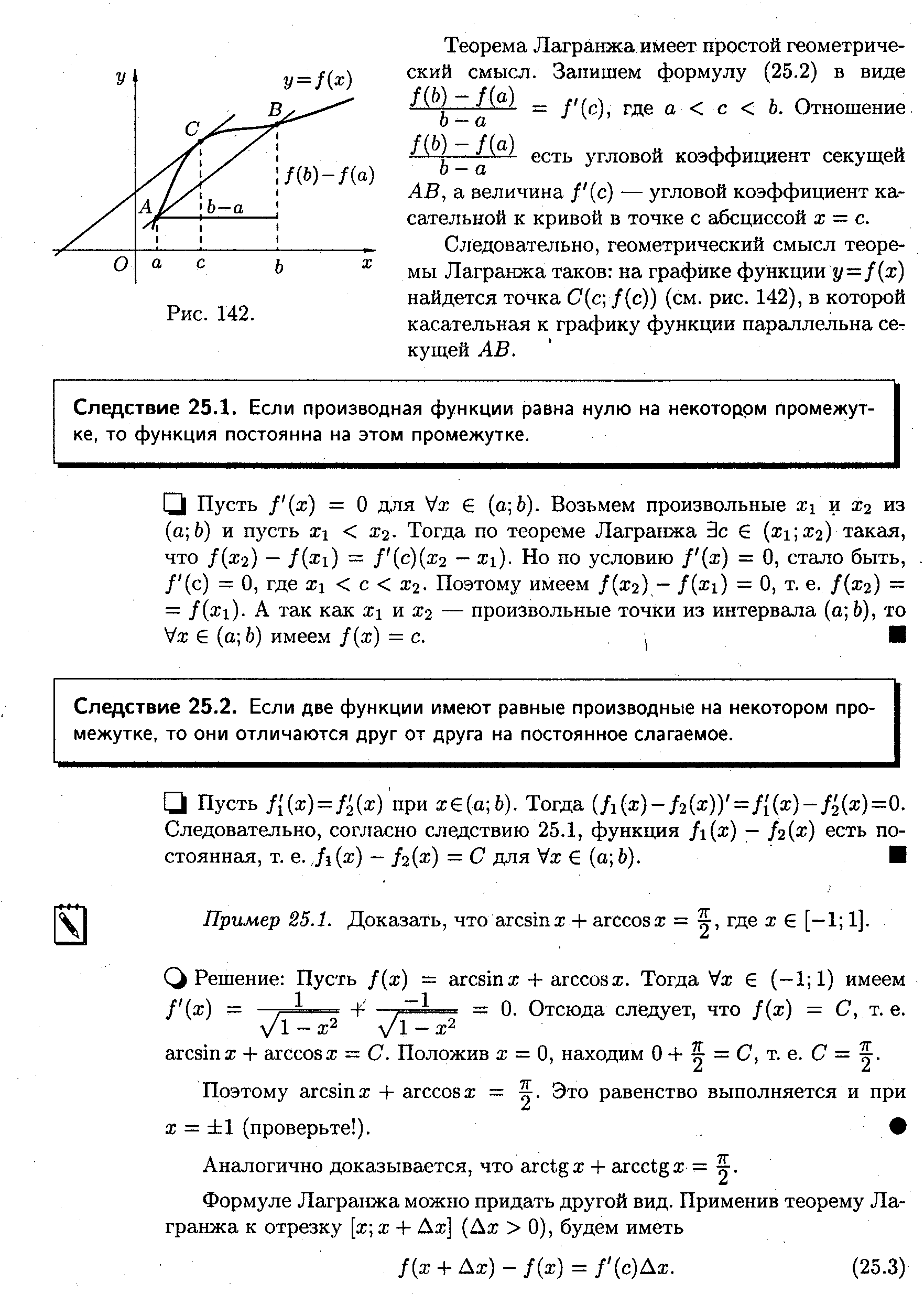
Рис. 142
рівно приросту аргументу, помноженому на значення похідної функції в деякій внутрішній точці цього відрізка.
Теорема Лагранжа має простий геометричний сенс. Запишемо формулу (7.1.2) у вигляді  , де . Відношення
, де . Відношення  є кутовий коефіцієнт січної АВ
є кутовий коефіцієнт січної АВ  , а величина – кутовий коефіцієнт дотичної до кривої в точці з абсцисою х=с.
, а величина – кутовий коефіцієнт дотичної до кривої в точці з абсцисою х=с.
Отже, геометричне значення теореми Лагранжа таке: на графіку функції знайдеться точка  (див. Рис. 142), в якій дотична до графіка функції паралельна січній АВ.■
(див. Рис. 142), в якій дотична до графіка функції паралельна січній АВ.■
Наслідок 7.1.1 Якщо похідна функції рівна нулю на деякому проміжку, то функція постійна на цьому проміжку.
□ Нехай  для
для  . Візьмемо довільні х1 і х2 з
. Візьмемо довільні х1 і х2 з  і нехай
і нехай 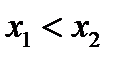 . Тоді по теоремі Лагранжа
. Тоді по теоремі Лагранжа 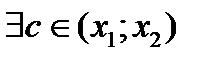 така, що
така, що  . Але по умові
. Але по умові  , отже,
, отже, 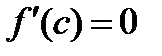 де
де  . Тому маємо
. Тому маємо  , тобто
, тобто  . А оскільки х1 і х2 - довільні точки з інтервалу
. А оскільки х1 і х2 - довільні точки з інтервалу  , то маємо
, то маємо 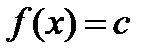 .■
.■
Наслідок 7.1.2. Якщо дві функції мають рівні похідні на деякому проміжку, то вони відрізняються один від одного на постійну сталу.
□ Нехай  при
при  . Тоді
. Тоді  . Отже, згідно слідству 25.1, функція
. Отже, згідно слідству 25.1, функція  є постійна, тобто
є постійна, тобто  для
для  ■
■
Приклад 7.1.1. Довести, що, де  .
.
○ Нехай 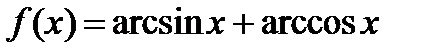 . Тоді маємо
. Тоді маємо  . Звідси витікає, що
. Звідси витікає, що  , тобто
, тобто 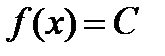 . Поклавши х=0, знаходимо
. Поклавши х=0, знаходимо  , тобто .
, тобто .
Тому  . Ця рівність виконується і при
. Ця рівність виконується і при 
Аналогічно доводиться, що .
Формулі Лагранжа можна надати інший вигляд. Застосувавши теорему Лагранжа до відрізка  , матимемо
, матимемо
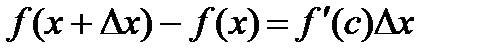 .
.
Кожне число можна записати у вигляді, де Формула (25.3) прийме вигляд
 ,
,
Виконуючи теорему Лагранжа, можна оцінити точність наближеної рівності . Зробимо це, вважаючи, що функція має не парну другу похідну :

 ,
,
де (Рис. 143).
Отже 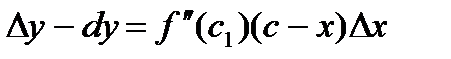 . Нехай . Оскільки
. Нехай . Оскільки 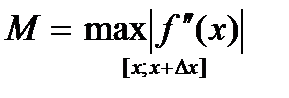 , а
, а  , то одержуємо оцінку
, то одержуємо оцінку 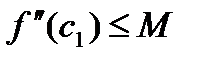 .●
.●

Рис. 143.
Правила Лопіталя
Розглянемо спосіб розкриття невизначеностей вигляду і, який заснований на застосуванні похідних.
Теорема 7.1.4. (правило Лопіталя розкриття невизначеностей вигляду  ). Нехай функція
). Нехай функція  і
і 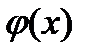 неперервна і диференційована в околі
неперервна і диференційована в околі  і обертаються в нуль в цій точці:
і обертаються в нуль в цій точці:  . Нехай
. Нехай  в околі точки
в околі точки  . Якщо існує границя
. Якщо існує границя  , то .
, то .
□ Застосуємо до функцій  і
і  теорему Коші для відрізка
теорему Коші для відрізка  , що лежить в околі точки хо . Тоді
, що лежить в околі точки хо . Тоді  , де с лежить між хо і х (Рис.144). Враховуючи, що
, де с лежить між хо і х (Рис.144). Враховуючи, що  , одержуємо
, одержуємо


При, величина з також прагне до ; перейдемо в рівності (25.4) до границі:
 .
.
Рис. 144.
Оскільки  , то . Тому
, то . Тому  .
.
Коротко отриману формулу читають так: межа відношення двох нескінченно малих рівна границі відношення їх похідних, якщо останній існує.■
Зауваження: 1. Теорема 7.1.4 вірна і у разі, коли функції і не визначені при, але і . Достатньо, поклавши, отримаємо
 .
.
3. Якщо похідні  і
і  , теорему 7.1.4 можна застосувати ще раз:
, теорему 7.1.4 можна застосувати ще раз:

і т.д.
Приклад 7.1.2. Знайти  .
.
○ 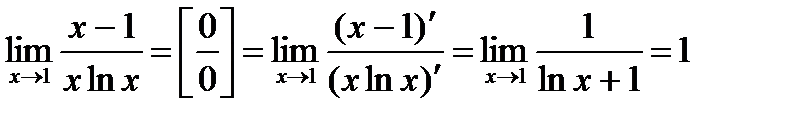 .●
.●
Приклад 7.1.3. Знайти  .
.
○  .●
.●
Теорема 7.1.4 дає можливість розкривати невизначеність вигляду  . Сформулюємо без доказу теорему про розкриття невизначеність вигляду .
. Сформулюємо без доказу теорему про розкриття невизначеність вигляду .
Теорема 7.1.5 (Правило Лопіталя розкриття невизначеностей вигляду 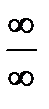 ). Нехай функції
). Нехай функції  і
і  неперервні і диференційовані в точці хо (окрім, може, бути, точки хо ), і в цьому околі
неперервні і диференційовані в точці хо (окрім, може, бути, точки хо ), і в цьому околі  ,
,  . Якщо існує границя
. Якщо існує границя 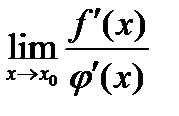 то
то  .
.
Приклад 7.1.4. Знайти 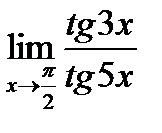 .
.
○ 

2-й спосіб:
 ●
●