 |
|
Максимум і мінімум функцій
Точка 
називається точкою максимуму функції, якщо існує такийокіл точки що для всіхз цієї околиці виконується нерівність 
.
Аналогічно визначається точка мінімуму функції: 
– точка мінімуму функції, якщо 
На малюнку 146
х1 – точка мінімуму, а точка х2 – точка максимуму функції .
Значення функції в точці максимуму (мінімуму) називається максимумом (мінімумом) функції. Максимум (мінімум) називається екстремумом функції.
Рис. 146
Поняття екстремуму завжди пов'язано з певною околицею точки з області визначення функції. Тому функція може мати екстремум лише у внутрішніх точках області визначення. Розглянемо умови існування екстремуму функції.
Теорема 7.1.8 (необхідна умова екстремуму). Якщо функція 
, що диференціюється, має екстремум в точці , то її похідна в цій точці рівна нулю 
.
□Нехай, для визначеності, – точка максимуму. Значить, в околиці точки виконується нерівність . Але тоді 
, якщо, і 
, якщо 
. По умові теореми похідна 
існує. Переходячи до границі, при, отримаємо 
, якщо
Рис. 147.
і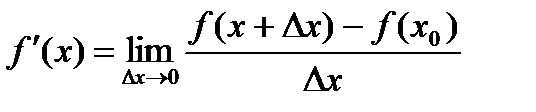 
, якщо . Тому . Аналогічно доводиться твердженя теореми 25.8, якщо – точка мінімуму функції .
Геометрично рівність означає, що в точці екстремуму функції 
, що диференціюється, дотична до її графіка
паралель до осі Ох (див. Рис. 147).
Відзначимо що зворотна теорема невірна, тобто якщо 
, то це не значить, що – точка екстремуму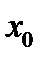 
.
Наприклад, для функції її похідна рівна нулю при х, але х не точка екстремуму (див. Рис. 148).
Існують функції, які в точках екстремуму не мають похідній. Наприклад, неперервна функція 
в точці х
Рис. 149. похідної не має,
але точка х 
– точка мінімуму (див. Рис. 149).
Таким чином, неперервна функція може має екстремум лише в точках, де похідна функції рівна нулю або не існує. Такі точки називаються критичними. ■
Рис. 148.
Теорема 7.1.9 (достатня умова екстремуму).Якщо неперервна функція диференціюється в деякому – околі критичної точки і під час переходу через неї (зліва направо) похідна міняє знак з плюса на мінус, то точка максимуму; з мінуса на плюс, то – точка мінімуму.
□Розглянемо 
– околиця точки . Нехай виконуються умови:
і . Тоді функція зростає на інтервалі, а на інтервалі вона убуває. Звідси витікає, що значення в точці є найбільшим на інтервалі, тобто для всіх . Це означає, що – точка максимуму функції.
Графічна інтерпретація доведення теореми 7.1.9 представлена на малюнку 150.
Рис.150.
Аналогічно теоремі 25.9 доводиться для випадку, коли і .
Досліджувати функцію на екстремум означає знайти всі її екстремуми. З теорем 7.1.8, 7.1.9 витікає наступне правило дослідження функції на екстремум:
1) знайти критичні точки функції ;
вибрати з них лише ті, які є внутрішніми точками області визначення функції;
2) досліджувати знак похідної зліва і справа до кожної з вибраних критичних крапок;
3) відповідно до теореми 25.9 (достатня умова екстремуму ) виписати точки екстремуму (якщо вони є) і обчислити значення функції в них.■
Приклад 7.1.9. Знайти екстремум функції .
○ Очевидно 
. Знаходимо, тобто 
.●
Похідна не існує при і рівна нулю при. Ці точки розбивають всю область визначення даної функції на три інтервали . Відзначимо на малюнку 151 знаки похідної зліва і праворуч від кожної з критичних крапок.
Рис. 151.
Отже, 
– точка максимуму, і =8– точка мінімуму .
Іноді буває зручним викорислтовувати іншу достатню ознаку існування екстремуму, засновану на визначенні знака другої похідної.
Теорема 7.1.10. Якщо в точці перша похідна функції рівна нулю і (), а друга похідна в точці існує і відмінна від нуля (), то при в точці функція має максимум і мінімум– при .
□Нехай для визначеності 
. Оскільки
,
то в достатньо малій околиці точки . Якщо, то, якщо, то .
Таким чином, під час переходу через крапку 
першу похідну міняє знак з мінуса на плюс. Отже, по теоремі 7.1.9, є точка мінімуму.
Аналогічно доводиться, що якщо , то в точці 
функція має максимуму.■