Главная | Обратная связь

Регрессионные методы

Регрессионные методыотносятся к методам статистического моделирования. В процессе статистического анализа и прогнозирования социально-экономических явлений необходимо количественно описать самые существенные взаимосвязи. Для достоверного отражения сущности и характера явлений и процессов следует выявлять причинно-следственные связи.

Причинная связь характеризуется временной последовательностью причины и следствия: причина всегда предшествует следствию. Для корректного понимания следует исключать совпадения событий, не имеющих причинной взаимосвязи.

Многие социально-экономические явления представляют результат одновременно и совокупно действующих причин. В таких случаях отделяются главные причины от второстепенных, несущественных.

Между явлениями различают два вида зависимостей: функциональную,или жестко детерминированную, и статистическую,или стохастически детерминированную.

Статистическая, или стохастическаязависимость, проявляется только в массовых явлениях, при большом числе единиц совокупности. При стохастической зависимости для заданных значений независимой переменной можно указать ряд значений , случайно рассеянных в интервале. Каждому фиксированному значению аргумента соответствует определенное статистическое распределение значений функции. Это связано с тем, что зависимая переменная, кроме выделенной переменной , подвержена влиянию также других неконтролируемых или неучтенных факторов, а также с тем, что накладываются ошибки измерения. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью. Появляющиеся значения зависимой переменной являются реализациями случайной величины.

Односторонняя стохастическая зависимость одной случайной переменной от другой или нескольких других случайных переменных рассматривается как регрессия. Функция, при помощи которой выражается односторонняя стохастическая зависимость, называется функцией регрессии или просто регрессией.

Существует различие между функциональной зависимостью и регрессией. Кроме того, что переменная при функциональной зависимости полностью определяет значение функции , функция обратима, т.е. существует обратная функция 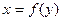. Функция регрессии таким свойством не обладает. Только в предельном случае, когда стохастическая зависимость переходит в функциональную зависимость, из одного уравнения регрессии можно перейти в другое.

Формализация вида уравнения регрессии неадекватна целям, связанным с измерениями в экономике и с анализом тех или иных форм зависимостей между переменными. Решение подобных задач становится возможным в результате введения в экономические соотношения стохастического члена: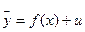

При изучении зависимостей следует иметь в виду, что функция регрессии только формально устанавливает соответствие между переменными, в то время как они могут не состоять в причинно-следственных отношениях. В этом случае могут возникнуть ложные регрессии вследствие случайных совпадений в вариациях переменных, которые не имеют содержательного смысла. Поэтому обязательным этапом перед подбором уравнения регрессии является качественный анализ зависимости между независимой переменной и зависимой переменной , основанный на предварительных гипотезах.

Относительно числа явлений (переменных), учитываемых в регрессии, различаются: простая (парная) и множественная регрессии.

Простая (парная) регрессия,то есть регрессия между двумя переменными. Одна переменная, подлежащая объяснению, является зависимой, результативной переменной или регрессандом.Другая независимая переменная, предсказывающая изменение зависимой, является факторным признаком или регрессором. Таким образом, простая регрессия есть односторонняя стохастическая зависимость результативной переменной только от одной объясняющей переменной. В уравнении справа находится оценка зависимой переменной, полученная на основе уравнения при некоторых усредненных условиях.

Множественная регрессия, то есть зависимость между переменной и несколькими причинно обусловленными объясняющими переменными 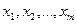. Функция регрессии . С помощью функции регрессии количественно оценивается усредненная зависимость между исследуемыми переменными.

Случайная переменная ,

, характеризует величину отклонения переменной от величины , вычисленной по функции регрессии . Случайная переменная называется возмущающей или, кратко, возмущением. Она включает влияние неучтенных факторов, случайных помех и ошибок измерения. Отдельные значения возмущающей переменной ведут себя случайным образом или рандомизированно.

Зависимую переменную можно представить в виде:

или

Такой вид записи позволяет интерпретировать случайную переменную как учитывающую неправильную спецификацию функции регрессии, т.е. неправильный выбор вида уравнения, описывающего зависимость.

Благодаря введению случайной переменной u , переменная y также становится случайной, поскольку ей нельзя при заданных значениях объясняющих переменных поставить в соответствие только одно определенное значение.