Главная | Обратная связь

Бесконечный числовой ряд и последовательность его частичных сумм. Сходящиеся и расходящиеся ряды.

Глава 1. Числовые ряды.

1.1 Бесконечный числовой ряд и последовательность его частичных сумм. Сходящиеся и расходящиеся ряды.

1.2 Остаток ряда.

1.3 Умножение ряда на число и сложение рядов.

1.4 Необходимый признак сходимости числового ряда. Гармонический ряд.

1.5 Ряды с положительными членами. Необходимый и достаточный признак сходимости таких рядов.

1.6 Достаточные признаки сходимости положительных рядов

п. 1. Признак сравнения.

п. 2. Признак Даламбера.

п. 3. Радикальный признак Коши.

п. 4. Интегральный признак Коши.

1.7 Знакочередующиеся ряды.

1.8 Критерий сходимости произвольных рядов.

1.9 Абсолютная и неабсолютная сходимость рядов.

1.10 Свойства сходящихся рядов.

1.11 Умножение рядов.

Вопросы для самоконтроля по главе 1.

Глава 2. Функциональные последовательности и ряды

2.1 Функциональные последовательности. Равномерная сходимость.

2.2 Функциональные ряды. Равномерная сходимость.

2.3 Признаки равномерной сходимости функциональных последовательностей и функциональных рядов.

2.4 Свойства равномерно сходящихся функциональных рядов и функциональных последовательностей.

2.5 Область сходимости степенного ряда.

2.6 Функциональные свойства суммы степенного ряда.

2.7 Задача разложения функции в степенной ряд. Единственность разложения. Формула Тейлора.

2.8 Формула Тейлора.

2.9 Условия разложимости функции в степенной ряд.

2.10 Разложение некоторых элементарных функций в степенной ряд.

2.11 Применение рядов к приближенным вычислениям.

Вопросы для самоконтроля по главе 2.

Контрольные задания.

Список рекомендуемой литературы.

 

Глава 1. Числовые ряды

Бесконечный числовой ряд и последовательность его частичных сумм. Сходящиеся и расходящиеся ряды.

Рассмотрим некоторую бесконечную последовательность чисел: Составленный из членов данной последовательности символ: 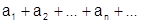(1) называется числовым рядом. Числа называются членами ряда, a_n - общий член ряда. Ряд принято обозначать так:
.

Станем последовательно складывать члены ряда (1), составляя суммы: Эти числа (2)
называются частичными суммами ряда (1).

Рассмотрим последовательность (2). Она может иметь конечный предел, может иметь бесконечный предел или совсем не иметь предела.

Определение.Если при 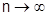последовательность (2) имеет конечный предел, то ряд (1) называется сходящийся, а число называется суммой ряда (1):

Определение.Если при 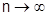последовательность (2) частичных сумм ряда (1) имеет бесконечный предел или не имеет предела, то ряд (1) называется расходящийся.

Таким образом, вопрос о сходимости ряда (1) равносилен вопросу о существовании конечного предела последовательности (2). И обратно, если мы рассмотрим последовательность , то вопрос о существовании конечного предела этой последовательности сводится к вопросу о сходимости следующего ряда: , (3)для которого ,... Таким образом, вопрос о существовании предела последовательности сводится к вопросу о сходимости ряда (3), для которого частичными суммами как раз и будут члены этой последовательности. При этом сумма ряда совпадает с пределом последовательности: .

Эти рассуждения показывают, что изучение бесконечного числового ряда есть просто новая форма изучения последовательности и ее предела.

Остаток ряда

Рассмотрим числовой ряд: . (1)

Отбросив в ряде (1) первые n членов, мы получим числовой ряд . (2)

Ряд (2) называется остатком ряда (1) после n-го члена.

Теорема 1.Если сходится ряд (1), то сходится и любой из его остатков. И обратно, если сходится какой-либо остаток ряда (1), то сходится и сам ряд (1).

Доказательство:
1) Пусть S - сумма сходящегося ряда (1). Для доказательства сходимости ряда (2) рассмотрим его k-ю частичную сумму W_k:

, где S_n и S_n+k – соответственно n-я и (n+k)-я частичные суммы ряда (1). Отметим, что здесь n - фиксированный номер, а k меняется. Переходя в последнем равенстве к пределу при k®¥, получим

.

Здесь мы учли, что в силу сходимости ряда (1) имеем: .

Итак, частичная сумма имеет конечный предел, т.е. ряд (2) сходится.

2) Пусть ряд (2) сходится. При фиксированном n ряд (2) представляет собой остаток ряда (1). Обозначим через сумму ряда (2), т.е. . Требуется доказать сходимость ряда (1). Имеем , т.е. (n+k)-я частичная сумма ряда (1) имеет конечный предел. Это и означает сходимость ряда (1).¨

Рассмотренную теорему можно было сформулировать и для расходимости.

Следствия:

1. Если ряд (1) сходится, то сумма его остатка после n-го члена стремится к нулю: .

2. Отбрасывание конечного числа начальных членов ряда или присоединение к ряду нескольких начальных членов не отражается на поведении ряда.