Главная | Обратная связь

Знакочередующиеся ряды

Признаки сходимости положительных рядов можно применять и к неположительным рядам в следующих двух случаях:

1. Ряд - отрицательный, т.е. . Почленное умножение ряда на число (-1) не влияет на ее сходимость, поэтому исследование сходимости ряда можно свести к исследованию сходимости положительного ряда .

2. Все члены ряда, кроме конечного их числа, имеют одинаковый знак. В этом случае, отбросив конечное число мешающих членов, можно получить знакопостоянный ряд, положительный или отрицательный.

 

В общем случае, когда имеется одновременно бесконечное множество отрицательных и бесконечное множество положительных членов, невозможно полностью изучить сходимость ряда только с помощью признаков сходимости положительных рядов. Требуются еще другие признаки.

Рассмотрим знакочередующиеся ряды

, (1)

, (2)

где все (здесь 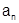- это модуль общего члена: или ), знаки строго чередуются.

Теорема 14 (теорема Лейбница - достаточный признак сходимости знакочередующегося ряда).Если модуль общего члена знакочередующегося ряда стремится к нулю, монотонно убывая, т.е. , то ряд сходится, и его сумма имеет знак первого члена и не превосходит его по модулю.

Доказательство.Рассмотрим частичную сумму ряда (1) на двух множествах: Е₁={2,4,…,2k,…} и E₂={1,3,…,2k-1,…}.

а)Пусть , т.е. . Тогда

, т.к. , причем, при переходе к частичной сумме добавляется слагаемое . Т.о. - положительная и возрастающая последовательность. Кроме того,

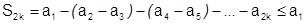, т.к. все скобки неотрицательны и . Поэтому согласно теореме о пределе монотонной последовательности ограниченная сверху числом возрастающая последовательность имеет конечный предел S.

С другой стороны, переходя в неравенстве к пределу при k®¥, получаем .

Итак, существует .

б) Пусть , т.е. .Тогда , но . Поэтому существует или существует .

Поскольку , то из а) и б) согласно теореме о пределах по множествам существует или просто . Этим сходимость ряда (1) доказана.

Аналогично доказывается сходимость ряда (2). Причем, оказывается, что .

Кроме того, для ряда (1): , для ряда (2): . Т.е. сумма S имеет знак первого члена . В любом случае или . ¨

Замечание: Условие монотонности в теореме существенно: если немонотонно, то ряд может и расходиться.

Примеры: 1)

Покажем, что этот ряд расходится:

, по , т.к. скобка – это частичная сумма гармонического ряда, который расходится. Отсюда следует, что последовательность не может иметь конечного предела (иначе частичная последовательность имела бы такой предел). Таким образом ряд расходится. Это объясняется тем, что нарушена монотонность убывания: при переходе от модуля каждого члена с четным номером к модулю следующего члена с нечетным номером, имеется возрастание (местное)

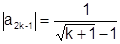
т.к. для .

Определение.Ряд, удовлетворяющий условиям теоремы Лейбница, называется рядом Лейбницевского типа.

Следствие: Любой остаток ряда Лейбницевского типа имеет знак своего первого члена и не превосходит его по модулю.

Доказательство.Любой остаток такого ряда есть снова ряд Лейбницевского типа и по доказанному его сумма имеет знак первого члена и .

Пример: Вычислить с точностью сумму ряда (точное значение суммы предполагается неизвестным).

Решение: это ряд Лейбницевского типа, поэтому сходятся к искомой конечной сумме S.

В качестве S возьмем частичную сумму со столькими членами, чтобы ошибка, т.е. модуль остатка был меньше но остаток , поэтому достаточно взять , .

Подберем n:

Годится . Значит .