Главная | Обратная связь

Умножение ряда на число и сложение рядов

Пусть дан ряд 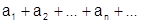. (1)

Определение.Умножить ряд (1) на число c- это значит умножить каждый член ряда (1) на число с.

Теорема 2.Если сходится ряд (1), то сходится и ряд (2), полученный из ряда (1) умножением его на число с, причем сумма ряда (2) будет c×S, где S- сумма ряда (1).

Доказательство:Нам дано, что . Обозначим через частичную сумму ряда (2):

.

Откуда

.¨

Теорема 3.Если ряд (1) расходится и c¹0, то и ряд (2) тоже расходится.

Доказательство:Допустим, что ряд (2) сходится. Тогда, умножив ряд (2) на число 1/c, мы получим ряд (1), который в силу теоремы 2 будет сходиться. Полученное противоречие и означает, что ряд (2) расходится. ¨

Рассмотрим наряду с рядом (1) ряд . (3)

Определение.Суммой рядов (1) и (3) будем называть ряд

. (4)

Разностью рядов (1) и (3) будем называть ряд

. (5)

Теорема 4. Если ряды (1) и (3) сходятся и их суммы соответственно равны А и В, то ряды (4) и (5) также сходятся и их суммы соответственно равны А+В и А-В.

Доказательство:

Нам дано: .

Обозначим через 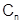частичную сумму ряда (4): .

Переходя к пределу при n®¥, имеем .

Аналогично доказывается для разности рядов.¨

Замечание.Теорема 3 справедлива и в случае сложения (разности) любого конечного числа сходящихся рядов.

1.4. Необходимый признак сходимости числового ряда.
Гармонический ряд

Теорема 5.Если ряд 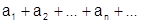(1) сходится, то .

Доказательство:Нам дано: . Из того, что , имеем: .¨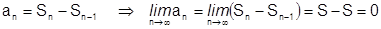

Необходимый признак сходимости числовых рядов можно использовать для установления расходимости ряда. В самом деле, если для какого-либо ряда , то ряд будет расходиться, т.к. если допустим, что ряд сходится, то по необходимому признаку сходимости мы должны получить, что , а это невозможно.

Теорема (Достаточный признак расходимости ряда).Если ряд (1) таков, что , то данный ряд расходится.

Следует твердо помнить, что необходимый признак сходимости рядов не является достаточным, т.е. даже при его выполнении ряд может расходиться.

Примером такого ряда является гармонический ряд: (2).

Покажем, что хотя 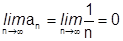, но , т.е. гармонический ряд расходится. Для этого рассмотрим последовательность с общим членом 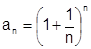, для которого . При доказательстве второго замечательного предела было показано, что возрастая, т.е. при любом n: .

Прологарифмируем последнее неравенство по основанию e:

,

т.е. . (3)

Учитывая неравенство (3), имеем

… …

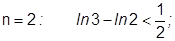
Сложив почленно все эти неравенства, получим: 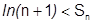. Т.к. , то подавно , т.е. гармонический ряд расходится.

1.5. Ряды с положительными членами.
Необходимый и достаточный признак сходимости таких рядов

Определение.Положительным рядом называется ряд вида 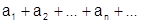, (1) где все .

Для рядов с положительными членами последовательность (S_n) частичных сумм является возрастающей последовательностью. В самом деле, рассмотрим S_n+1 и S_n: S_n+1=S_n+a_n+1 ; следовательно S_n+1 ³ S_n , т.к. a_n+1³0. Если вспомним теорему о пределе монотонной последовательности, то для сходимости последовательности частичных сумм достаточно, чтобы эта последовательность была ограничена сверху. Приходим к следующей теореме.

Теорема 6 (необходимый и достаточный признак сходимости положительного ряда).Для сходимости положительного ряда (1) необходимо и достаточно, чтобы последовательность 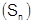его частичных сумм была ограничена сверху.

Доказательство:
Необходимость: Из того, что ряд (1) сходится, следует существование конечного предела , что равносильно тому, что .

Откуда получаем, что 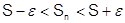для .

Обозначим через М наибольшее из чисел S+e,S₁,S₂,…,S_N(e) :
M= max{ S+e, S₁,S₂,…,S_N(e) }. Тогда 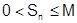для всех , т.е. 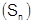ограничена сверху.

Достаточность: Т.к. 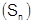- монотонная и ограниченная сверху последовательность, то по теореме о пределе монотонной и ограниченной последовательности имеем: - т.е. ряд (1) сходится.¨

Доказанная теорема непосредственно редко применяется на практике, но все достаточные признаки сходимости положительных рядов выводятся на основе этой теоремы.