Главная | Обратная связь

П. 1. Признак сравнения

Сходимость или расходимость положительного ряда часто удается установить путем его сравнения с другим рядом, сходимость или расходимость которого известна или легко может быть установлена.

Во многих случаях исследуемые ряды сравниваются с так называемыми рядами - эталонами для сравнения: , ,

(который сходится при p>1 и расходится при p£1).

Такое сравнение положительного ряда с другим рядом, сходимость или расходимость которого известна, основано на следующей теореме:

Теорема 7.Пусть даны два положительных ряда:

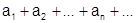, (1) . (2). Если, хотя бы начиная с некоторого номера n>N, выполняется неравенство , то из сходимости ряда (2) следует сходимость ряда (1) и из расходимости ряда (1) следует расходимость ряда (2).

Доказательство:
1) Пусть ряд (2) сходится. На основании того, что отбрасывание конечного числа начальных членов ряда не отражается на поведении ряда, можно считать, что неравенство 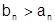(3)выполняется для всех номеров, начиная с первого.

Обозначим через A_n и B_n n-е частичные суммы рядов (1) и (2) соответственно. На основании неравенства (3) имеем: (4)

Из того, что ряд (2) сходится, следует, что ограничена сверху: . Тогда на основании неравенства (4) подавно , т.е. ряд (1) сходится.

2) Из того, что ряд (1) расходится, следует: . Тогда на основании неравенства (4) подавно 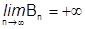, что означает расходимость ряда (2).¨

Пример: Исследовать на сходимость ряд:

Решение: будем сравнивать с рядом геометрической прогрессии. - общий член геометрической прогрессии, где , ; ряд геометрической прогрессии сходится 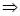по 1 признаку сравнения ряд сходится.

На практике часто признак сравнения применяют в предельной форме.

Теорема 8.Если существует конечный предел , где k>0, то ряды (1) и (2) сходятся или расходятся одновременно.

Доказательство:
1) Пусть ряд (2) сходится и . Из того, что предел существует, на основании определения предела имеем:

.

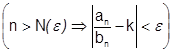Откуда следует: или , но ряд (2) сходится, тогда, умножая его на число , получим также сходящийся ряд с общим членом . Тогда по теореме 7 ряд (1) с меньшим общим членом тоже сходится.

2) Пусть ряд (2) расходится и , следовательно, . Тогда на основании определения предела: для , откуда . Отсюда следует, что ряд (1) должен расходиться, иначе бы сходился полученный из ряда (1) умножением на число ряд , а значит и ряд (2) как ряд с меньшими членами.

Пример: исследовать на сходимость ряд .

Решение: будем сравнивать с гармоническим рядом: , .

(конечное число), тогда по теореме 8 данный ряд есть ряд расходящийся.