 |
|
Глава 2. Функциональные последовательности и ряды.
2.1. Функциональные последовательности.
Равномерная сходимость
Рассмотрим функциональную последовательность (ФП)
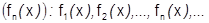, (1), где 
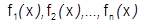- функции, заданные на общем множестве Х. При каждом конкретном 
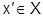имеем числовую последовательность: 
, которая может сходиться или расходиться. Если она сходится, то говорят, что ФП (1) сходится в точке x’.
Определение. Множество всех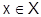 
, в которых ФП (1) сходится, называют областью сходимости ФП (1).
Пусть Е - область сходимости ФП (1). Ясно, что 
. В этом случае говорят, что ФП (1) сходится на множестве Е. При каждом 
получается числовая последовательность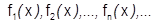 
, сходящаяся к некоторому числу, зависящему от x, обозначим его через 
.
Получается функция 
, определенная на множестве Е. Ее называют предельной функцией для ФП (1).
Представляет интерес вопрос: сохраняются ли функциональные свойства функции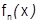 
(переход к пределу, непрерывность, дифференцируемость, интегрируемость) после перехода к предельной функции .Примеры показывают, что в общем случае это не имеет место.
Пример . Рассмотрим ФП 
на множестве 
. Очевидно, 
.
а) при 
б) при 
.
Следовательно, 
т.е. предельная функция уже не является непрерывной - в точке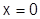 
терпит разрыв.
Оказывается, что сохранение функциональных свойств функции 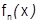после перехода к предельной функции будет обеспечено при особом характере сходимости ФП (1) на всем множестве Е.
Пусть ФП (1) сходится на множестве Е к предельной функции . Это значит, что при каждом конкретном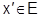 
числовая последовательность сходится к числу 
, именно
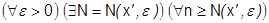
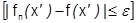
где номер N зависит не только от e, но и от x’, т.е. для каждого x’ находится, вообще говоря, свой номер N.
Может оказаться, что можно найти один номер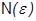 
, годный сразу для всех одновременно, т.е. такой номер 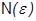, что какое бы ни взять, всегда
.
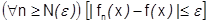В этом случае говорят, что ФП (1) к предельной функции сходится равномерно на множестве Е.
Определение 1. Пусть ФП (1) сходится на множестве Е к предельной функции . Если для любого 
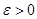можно найти номер 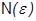такой, что при всех 
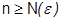выполняется неравенство 
сразу для всех одновременно, то говорят, что ФП (1) сходится к равномерно на множестве Е и пишут: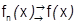 
на Е:
В противном случае, если для какого-либо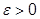 
не существует номера N, который бы при 
обеспечивал неравенство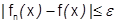 
для 
одновременно, говорят, что ФП сходится к предельной функции неравномерно.
Замечание 1.Как известно, если 
, то 
; обратно, очевидно: 
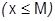. Следовательно, эти два утверждения равносильны:
.
Поэтому вместо условия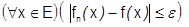 
можно взять 
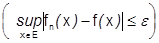. Тогда получаем:
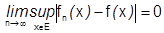
или, если обозначим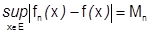 
, то 
.
Дадим теперь равносильное
Определение 2. Если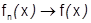 
на множестве Е, то говорят, что 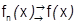на Е, если , т.е. 
.
Замечание 2.Из определений видно, что говорить о равномерной сходимости в одной отдельно взятой точке не имеет смысла, т.к. это понятие относится ко всему множеству Е в целом. В отличии от равномерной сходимости сходимость в каждой отдельной точке называют поточечной сходимостью.
Определения предполагают, что равномерная сходимость возможна только при поточечной сходимости, т.е. если ФП равномерно сходится на Е, то она сходится в каждой отдельной точке Е. Обратное, вообще говоря, неверно: поточечная сходимость еще не влечет равномерной сходимости.
Пример 1: 
, 
.
– предельная функция, следовательно, поточечная сходимость имеется.
На чертеже показана сходимость функциональной последовательности в конкретной точке 
(будет ли равномерной?).
-?
непрерывны на 
и согласно 2-й теореме Вейерштрасса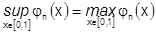 
Исследуя 
при помощи производной, находим что 
.
Таким образом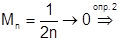 
сходимость равномерная.
Пример 2 (покажем, что равной сходимости нет).
, 
 |
- как в примере 1 предельная функция тажа: 
, т.е. поточечная сходимость есть.
, но здесь: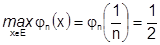 
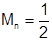не стремится к 0 
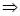сходимость неравномерная.
Если, например, возьмем 
, то не найдется номера N который бы сразу для всех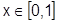 
обеспечивал при 
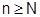неравенства 
. В самом деле: какой бы N ни взять всегда при 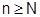это неравенство выполняется не для всех 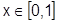одновременно, именно, для 
оно не выполнится: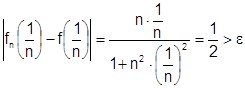 
.
Здесь при каждом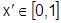 
соответствующие точки 
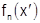на графиках 
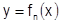неограниченно приближаются к точкам 
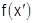, однако при 
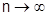весь график 
сразу по всему участку: всегда остается просвет между границами (высотой ½). Отметим, что в других случаях подобный просвет может даже возрастать до 
.