Главная | Обратная связь

Свойства равномерно сходящихся функциональных рядов и функциональных последовательностей.

Теорема 26 (о непрерывности суммы функционального ряда).Если ряд непрерывных функций сходится к сумме равномерно на множестве Е, то сумма ряда – функция – непрерывна на Е.

Доказательство: надо доказать, что непрерывна в произвольной т. , т.е. . Зададим . По условию на Е. Поэтому такой, что . Возьмем . Для него тоже 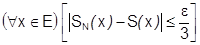. В частности это верно при 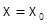: . Рассмотрим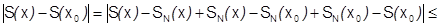

Но функция - как конечная сумма N непрерывных функций непрерывна в точке 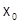, поэтому:

. В итоге по заданному нашли , такое, что , что и требовалось доказать.¨

Теорема 26' (о непрерывности предельной функции последовательности). Если последовательность непрерывных функций сходится к предельной функции f(x) равномерно на Е, то предельная функция f(x) непрерывна на Е.

Отметим, что условие равномерной сходимости в теоремах 26' и 26 достаточное, но не является необходимым: может оказаться, что сумма ряда непрерывных функций или соответствующая предельная функция последовательности непрерывных функций непрерывна на множестве Е даже в случае неравномерной сходимости.

Например, последовательность 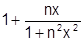непрерывных функций сходится к непрерывной функции , хотя сходимость неравномерная (см. пример 2.1).

Теорема 27 (о почленном интегрировании ряда). Если ряд непрерывных функций сходится к сумме 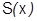равномерно на отрезке , то его можно почленно интегрировать по любому отрезку

, т.е. ряд из интегралов сходится к интегралу от суммы.

Доказательство: надо доказать, что числовой ряд 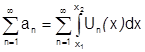сходится к сумме , т.е. или (*).
Заметим, что существуют [ряд сходится на равномерно] .
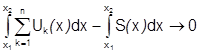
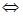
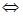
Учитывая, что конечную сумму можно почленно интегрировать, требуемое условие (*) можно переписать в виде: 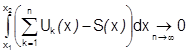. По условию 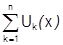равномерно сходится к 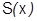на . Поэтому существует номер такой, что сразу на всем отрезке 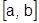, в частности и на .

Поэтому при имеем .

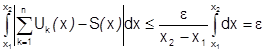Таким образом: .¨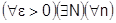

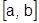Теорема 27’ (о почленном интегрировании функциональной последовательности).Если последовательность непрерывных функций сходится к предельной функции равномерно на , то 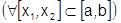, т.е. можно перейти к пределу под знаком интеграла.

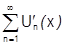Теорема 28 (о почленном дифференцировании ряда).Пусть ряд непрерывно дифференцируемых функций сходится к сумме на . Если ряд производных сходится на равномерно, то данный ряд можно почленно дифференцировать на . , т.е. ряд из производных сходится к производной суммы ряда.

Доказательство: пусть - сумма 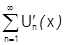: 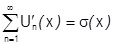Надо доказать, что существуют и это 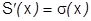. По условию функции непрерывно дифференцируемые, т.е. непрерывна на .

Кроме того, ряд сходится равномерно, поэтому по теореме 26 сумма ряда непрерывна, а по теореме 27 его можно почленно интегрировать по любому отрезку из . Проинтегрируем по :

.

По условию сходится при , в частности при 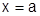, т.е. сходится ряд . Почленно вычитая эти ряды, получим: .

Отсюда: или . По теореме о дифференцируемости интеграла с переменным верхним пределом, благодаря непрерывности на производная существует и равна . Поэтому существует и , что и требовалось доказать.¨

Теорема 28’.Пусть последовательность непрерывно дифференцируемых функций сходится на к функции . Если последовательность производных 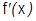сходится на этом отрезке равномерно, то 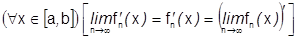, т.е. можно перейти к пределу под знаком производной.