 |
|
Признаки равномерной сходимости функциональных последовательностей и функциональных рядов.
Теорема 23 (критерий Коши равномерной сходимости функциональной последовательности). Для того чтобы функциональная последовательность 
(1) сходилась на множестве 
равномерно, необходимо и достаточно, чтобы по любому заданному 
можно было указать такой номер 
(независящий от х), что сразу для всех 
выполнялось неравенство: 
при любых 
:
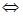
Доказательство:
Необходимость: Пусть 
равномерно сходится на множестве , то есть сходится к некоторой предельной функции 
: 
.
По определению 1 (смотри 2.1) по произвольно заданному 
такой, что 
. В частности, это, верно при всех 
и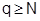 
: 
.
Достаточность: Пусть критерий выполнен. При каждом конкретном он представляет собой известный критерий Коши для числовой последовательности: 
и благодаря выполнению этого критерия числовая последовательность сходится к некоторому числу, зависящему от 
, обозначим его 
. Это значит, что функциональный ряд (1) поточечно сходится на множестве к некоторой предельной функции . Докажем, что эта сходимость равномерная.
Зададим . Согласно критерию 
, такой, что 
.
Возьмем фиксированное , для него тоже при всех 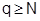имеем: 
Устремим теперь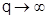 
, при этом процессе последнее неравенство сохраняется при этом 
т.к. 
, а 
- в силу доказанной поточечной сходимости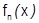 
к .
.
.
Таким образом: при каждом получим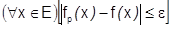 
.
Так что: 
(по определению 1 см. 2.1) [(1) сходится равномерно].
Переформулируем теорему для функционального ряда:
Теорема 24 (критерий Коши равномерной сходимости функционального ряда).[Ряд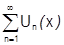 
сходится равномерно на ] 
.
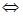
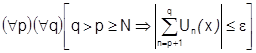Если ряд равномерно сходится на множестве , то критерий Коши выполняется в частности и для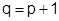 
. В этом случае 
.
Кроме того: 
.
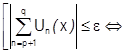
Поэтому получается следствие (необходимый признак сходимости ряда):
[Ряд 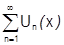сходится равномерно на ] 
.
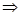
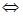
Функциональный ряд может равномерно сходиться на множестве только тогда, когда последовательность верхних граней модуля общего члена сходится к 0, т.е. общий член сходится к 0 равномерно на множестве .
Пример 1. 
; 
.
При каждом фиксированном 
при достаточно больших 
будет 
поэтому ряд можно считать положительным.
Применим к исследованию поточечной сходимости признак сравнения. Сравним с рядом 
(сход).
, 
.
Значит, ряд поточечно сходится на .
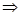не стремится к 0 сходимость неравномерная.
Теорема 25 (достаточный признак Вейерштрасса равномерном сходимости ряда).Если для данного функционального ряда 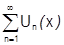(2) существует сходящийся положительный числовой ряд 
(3) такой, что 
, (4) то функциональный ряд (2) сходится на абсолютно и равномерно.
При выполнении (4) говорят, что функциональный ряд мажорируется числовым рядом, числовой ряд (3) называют мажорантным или мажорантой.
Доказательство: по признаку сравнения (4)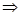 
сходится 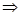(2) абсолютно сходится.
Равномерная сходимость устанавливается по признаку Коши (теорема 24). Зададим . Для сходящегося числового ряда (3) выполняется свой критерий Коши, согласно которому существует номер такой, что 
, причем не зависит от , т.к. (3) – числовой ряд. Складывая конечное число неравенств (4), получим 
. Отсюда: 
.
Таким образом: 
– критерий Коши равномерной сходимости выполняется 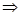ряд (2) сходится равномерно.¨
Пример 2: 
.
.
- сходится, следовательно данный ряд сходится абсолютно и равномерно на 
.
Замечание:Признак Вейерштрасса можно применить только к абсолютно сходящимся рядам, т.к. при выполнении этого признака ряд обязательно сходится и абсолютно.
Пример 3: 
. Этот ряд Лейбницевского типа, следовательно сходится на Е, но сходимость не абсолютная, т.к. ряд из модулей 
расходится (можно сравнить с гармоническим рядом 
). Установим равномерную сходимость по определению 3 см. 2.2 (признак Вейерштрасса не подходит).
ряд сходится равномерно.