 |
|
Абсолютная и неабсолютная сходимость рядов.
Иногда при изучении сходимости произвольного ряда  (1)
(1)
помогает ряд, составленный из модулей его членов:  .(2)
.(2)
Определение. Если ряд (1) сходится одновременно с рядом (2), то говорят, что ряд (1) сходится абсолютно.
Для положительных рядов понятия сходимости и абсолютной сходимости совпадают, т.к. для них  . В общем случае, не каждый сходящийся ряд сходится абсолютно.
. В общем случае, не каждый сходящийся ряд сходится абсолютно.
Пример 1: Рассмотрим ряд  - это ряд Лейбницевского типа, он сходится. Ряд из модулей его членов
- это ряд Лейбницевского типа, он сходится. Ряд из модулей его членов 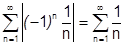 - гармонический ряд, он расходится, т.е. абсолютной сходимости нет.
- гармонический ряд, он расходится, т.е. абсолютной сходимости нет.
Пример 2:  – это ряд Лейбницевского типа, он сходится. Ряд из модулей:
– это ряд Лейбницевского типа, он сходится. Ряд из модулей: 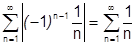 – гармонический ряд, он расходится.
– гармонический ряд, он расходится.
Определение. Сходящийся ряд, несходящийся абсолютно, называется неабсолютно сходящимся (условно сходящимся).
Так ряд в примере 1 - неабсолютно сходящийся.
Оказывается, сходимость ряда из модулей (2) всегда влечет сходимость самого ряда (1).
Теорема 16 (теорема Коши об абсолютной сходимости ряда). Если ряд из модулей (2) сходится, то сходится и сам ряд (1), и его сумма A=P-Q, где P - сумма ряда, состоящего из неотрицательных членов 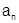 , Q - сумма ряда, составленного из модулей отрицательных членов
, Q - сумма ряда, составленного из модулей отрицательных членов 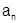 .
.
Доказательство. Построимдва положительных ряда  и
и 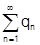 следующим образом: в качестве суммы
следующим образом: в качестве суммы  возьмем ряд (1), в котором неотрицательные члены
возьмем ряд (1), в котором неотрицательные члены 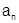 сохраним, а отрицательные члены заменим нулями:
сохраним, а отрицательные члены заменим нулями: 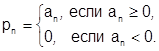 В качестве суммы
В качестве суммы 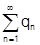 возьмем ряд (1), в котором неотрицательные члены
возьмем ряд (1), в котором неотрицательные члены 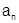 заменим нулями, а отрицательные члены заменим их модулями:
заменим нулями, а отрицательные члены заменим их модулями:

По построению всегда 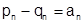 ; в любом случае
; в любом случае 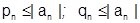 . Из последних неравенств и в силу сходимости ряда
. Из последних неравенств и в силу сходимости ряда  по признаку сравнения сходятся положительные ряды
по признаку сравнения сходятся положительные ряды  и
и 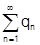 . Эти сходящиеся ряды можно почленно вычитать. Получится снова сходящийся ряд. При этом, если
. Эти сходящиеся ряды можно почленно вычитать. Получится снова сходящийся ряд. При этом, если 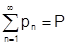 и
и 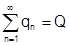 , то
, то 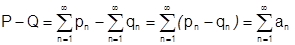 . Таким образом, ряд (1) сходится:
. Таким образом, ряд (1) сходится:
 . ¨
. ¨
Замечание. Поскольку ряд из модулей (2) положительный, то при исследовании абсолютной сходимости ряда (1) можно пользоваться всеми признаками сходимости положительных рядов (сравнения, Даламбера, радикальный и интегральный признаки Коши). Нужна только осторожность при расходимости ряда (2), т.к. если даже ряд (2) расходится, сам ряд (1) может сходиться (неабсолютно). Исключение составляют только признак Даламбера и радикальный признак Коши. Если расходимость ряда из модулей (2) установлена с помощью этих признаков, то, как это видно из доказательств этих признаков, расходимость имеет место из-за нестремления 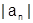 к нулю. Но при этом и само
к нулю. Но при этом и само 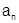 не стремится к нулю, т.е. ряд (1) тоже расходится.
не стремится к нулю, т.е. ряд (1) тоже расходится.
Таким образом, применение этих двух признаков к ряду из модулей (2) полностью решает вопрос о сходимости или расходимости ряда (1), поэтому эти признаки можно сформулировать для произвольного ряда.
Теорема 17 (признак Даламбера (Коши) для произвольного ряда). Если при всех достаточно больших n 
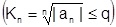 , где
, где 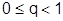 , то ряд (1) сходится; если при достаточно больших n
, то ряд (1) сходится; если при достаточно больших n  , то расходится.
, то расходится.
Следствие. Если существует 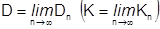 , то при
, то при 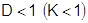 ряд (1) сходится; при
ряд (1) сходится; при  - расходится; при
- расходится; при  вопрос остается открытым.
вопрос остается открытым.
Пример 2:  (сходится или расходится?)
(сходится или расходится?)
Возьмем 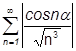 .
.
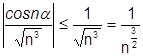
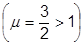

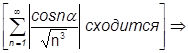
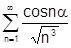 сходится, т.е. данный ряд абсолютно сходится. Данный ряд не знакопостоянен т.к.
сходится, т.е. данный ряд абсолютно сходится. Данный ряд не знакопостоянен т.к.  может менять знак.
может менять знак.
Пример 3: Установить, при каких х расходится ряд  .
.
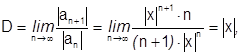 ряд расходится при
ряд расходится при 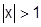 :
:  . Например,
. Например,  - расходится.
- расходится.