 |
|
Функциональные ряды. Равномерная сходимость
Пусть 
- (1) функциональный ряд (ФР), где члены ряда 
- функции, определенные на общем множестве Х.
При каждом конкретном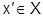 
получаем числовой ряд. Множество 
всех точек x, при подстановке которых в ФР (1) получаются сходящиеся числовые ряды, называется областью сходимости ФР.
Частичная сумма 
зависит от выбора x, т.е. является функцией от x:
.
Поэтому и сумма ряда (1) оказывается зависящей от выбора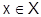 
, т.е. оказывается функцией, определенной на множестве Е:
.
Как известно, изучение ряда есть просто другая форма исследования последовательности, т.к. от последовательностей легко перейти к рядам и обратно:
| Функциональная последовательность | Функциональный ряд | |
| 
| 
|
| 
| 
|
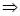
Поэтому всякое утверждение, доказанное для ФП, с соответствующими изменениями формулировки переносится и на ряд и обратно.
Как и для ФП-й сохранение функциональных свойств функции после перехода к сумму ряда 
будет обеспечено при равномерной сходимости ФР.
Определение 1.ФР (1), сходящийся на множестве Е к сумме называется равномерно сходящимся на этом множестве, если равномерно сходится на Е последовательность его частичных сумм:
на Е.
Поскольку 
- остаток ряда, то на Е 
на Е. Действительно,
на Е 
.
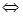
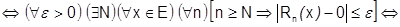
Определение 2. ФР (1), сходящийся на множестве Е к сумме называется равномерно сходящимся на этом множестве, если последовательность его остатков равномерно сходится к нулю на Е.
Согласно определению 2 из 2.1.: [ ] на Е 
.
Определение 3. ФР (1), сходящийся на множестве Е к сумме , называется равномерно сходящимся на этом множестве, если последовательность верхних граней модулей его остатков сходится к нулю.
Замечания 1 и 2 в 2.1. сохраняют силу и для ФР.
Пример. 
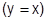сходится при 
, т.е. на множестве 
, 
.
.
Остаток ряда не ограничен т.к. при 
получаем 
, значит 
сходимость не равномерная.