 |
|
Область сходимости степенного ряда.
Функциональный ряд 
 , где
, где  - вещественные коэффициенты,
- вещественные коэффициенты, 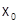 - фиксированное вещественное число, называется степенным рядом (по степеням
- фиксированное вещественное число, называется степенным рядом (по степеням  ).
).
Заменяя: 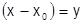 , приходим к ряду
, приходим к ряду  , поэтому обычно будем рассматривать
, поэтому обычно будем рассматривать 
 (1) – степенной ряд по степеням
(1) – степенной ряд по степеням  .
.
Изучим область сходимости ряда (1). Ясно, что при 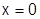 сходится любой степенной ряд (1) к сумме
сходится любой степенной ряд (1) к сумме  . Существуют степенные ряды, которые не сходятся ни в какой другой точке, кроме
. Существуют степенные ряды, которые не сходятся ни в какой другой точке, кроме 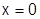 .
.
Пример 1: 
 .
.
По признаку Коши: 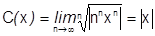


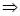 ряд расходится при всех
ряд расходится при всех  .
.
Существуют ряды, сходящиеся при  .
.
Пример 2:  .
.
 ,
,  ряд сходится
ряд сходится  .
.
Существуют степенные ряды, которые сходятся при одних значениях  и расходятся при других значениях
и расходятся при других значениях  .
.
Уточнить область сходимости поможет:
Теорема 29 (Абеля)Если степенной ряд (1) сходится при некотором значении  , то он сходится и притом абсолютно при всех значениях
, то он сходится и притом абсолютно при всех значениях  , для которых
, для которых  , т.е. в интервале
, т.е. в интервале  .
.
Если же ряд (1) расходится при некотором 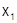 , то он расходится при всех
, то он расходится при всех  , для которых
, для которых  , т.е. на интервалах
, т.е. на интервалах  ,
, 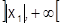 .
.

Доказательство:
1) Пусть ряд (1) сходится в точке  , тогда
, тогда 
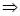

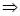 [последовательность
[последовательность 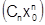 ограничена]
ограничена] 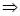
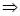

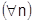
 .
.
Рассмотрим ряд в точке  , для которого
, для которого  .
.
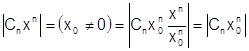

но геометрический ряд  при
при  сходится
сходится 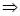 сходится и ряд
сходится и ряд  , а это означает абсолютную сходимость ряда (1).
, а это означает абсолютную сходимость ряда (1).
2) Если ряд (1) расходится в некоторой точке 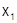 , то при
, то при  ряд не может сходиться в точке
ряд не может сходиться в точке  , иначе, по доказанному, он бы сходился в точке
, иначе, по доказанному, он бы сходился в точке 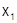 с меньшим модулем.
с меньшим модулем.
Теорема 30 (об интервале сходимости степенного ряда). Для каждого степенного ряда (1) существует такое число R, 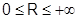 , что в интервале
, что в интервале 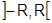 ряд (1) сходится абсолютно, а вне интервала расходится.
ряд (1) сходится абсолютно, а вне интервала расходится.
Доказательство:
I. Если ряд сходится только в точке 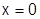 , то можно считать, что
, то можно считать, что  есть интервал
есть интервал 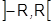 при
при  .
.
Причем, сходимость в точке 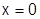 абсолютная (
абсолютная (  - сходится к
- сходится к  ), поэтому в этом случае утверждение теоремы верно.
), поэтому в этом случае утверждение теоремы верно.
II. Пусть существуют точки сходимости, отличные от 0, обозначим такие точки через  . Возьмем
. Возьмем  (
(  всегда существует, конечный или бесконечный).
всегда существует, конечный или бесконечный).
По условию имеется хотя бы одно  . Для него
. Для него  (т.к.
(т.к.  ). Поэтому тем более
). Поэтому тем более 
 .
.
Рассмотрим интервал 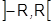 . Для него найдется такая точка
. Для него найдется такая точка  , что
, что  , т.к. в противном случае было бы:
, т.к. в противном случае было бы: 

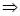

 вместо
вместо  на интервале
на интервале 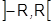 но С есть точка сходимости, отличная от 0 и согласно теореме Абеля неравенство:
но С есть точка сходимости, отличная от 0 и согласно теореме Абеля неравенство:  влечет абсолютную сходимость в точке
влечет абсолютную сходимость в точке  .
.
Таким образом в  ряд абсолютно сходится.
ряд абсолютно сходится.
Если 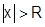 (это возможно только при
(это возможно только при  ), то
), то  не может быть точкой сходимости, т.к. для точек сходимости С должно быть
не может быть точкой сходимости, т.к. для точек сходимости С должно быть  .
.
Следовательно, вне интервала  ряд расходится. Интервал
ряд расходится. Интервал  называется интервалом сходимости, а число
называется интервалом сходимости, а число  радиусом сходимости степенного ряда.
радиусом сходимости степенного ряда.
В точках  и
и  по отдельности ряд (1) может сходиться (абсолютно или неабсолютно) или расходиться.
по отдельности ряд (1) может сходиться (абсолютно или неабсолютно) или расходиться.
Таким образом получается:
Теорема 31 (об области сходимости степенного ряда). Область сходимости степенного ряда (1) есть его интервал сходимости возможно с добавлением одного или обоих его концов.
Замечания:
1) Для степенного ряда общего вида  интервал сходимости имеет вид
интервал сходимости имеет вид  , т.к. заменой
, т.к. заменой  приходим к ряду
приходим к ряду  с интервалом сходимости
с интервалом сходимости  и неравенства
и неравенства 
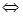

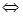
 .
.
2) Множество точек, в которых произвольный функциональный ряд абсолютно сходится, называется областью абсолютной сходимости.
Для степенного согласно теореме 31 оказывается, что область абсолютной сходимости совпадает с областью простой сходимости, с точностью до границ интервалов сходимости (на этих границах сходимость может быть неабсолютной).
Интервал сходимости можно найти, применяя признак Даламбера или радикальный признак Коши (если соответствующие пределы существуют). Дополнительно исследовав сходимость на концах интервала, можно установить область сходимости ряда (1).
Пример: Найти область сходимости степенного ряда  .
.
(пр. Даламбера): 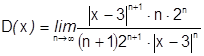
 ряд абсолютно сходится при
ряд абсолютно сходится при 
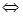

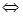
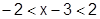
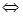
 . Ряд расходится при
. Ряд расходится при 
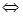 …
… 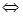
 .
.
Таким образом интервал сходимости  ,
, 
Исследуем поведение ряда на концах интервала:
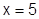 :
:  – расходится.
– расходится.
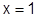 :
:  – Лейбницевского типа – сходится, но сходимость неабсолютная, т.к. ряд
– Лейбницевского типа – сходится, но сходимость неабсолютная, т.к. ряд  расходится.
расходится.
Область сходимости  .
.