Главная | Обратная связь

Функциональные свойства суммы степенного ряда.

Теорема 32 (о равномерной сходимости степенного ряда). Степенной ряд 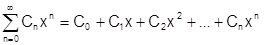(1) на каждом отрезке интервала сходимости сходится равномерно.

Доказательство:
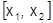– произвольный отрезок интервала сходимости , .

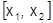
Поместим отрезок 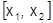в симметричный отрезок .

В точке ряд сходится абсолютно, т.е. сходится ряд .
, но это означает, что ряд (1) на отрезке мажорируется положительно сходящимся числовым рядом и по принципу Вейерштрасса (теорема 25 2.3) ряд (1) сходится на равномерно и тем более на 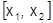, входящем в .¨

Теорема 33 (о функциональных свойствах суммы степенного ряда). Сумма степенного ряда (1):

1)непрерывна на интервале сходимости.

2)интегрируема по любому отрезку 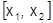интервала сходимости, причем получается почленным интегрированием ряда (1): ;

3) бесконечно дифференцируема на интервале сходимости, причем к-я производная от суммы получается k-кратным почленным дифференцированием ряда (1):

.

Доказательство: для имеем: и по теореме 32 ряд сходится на равномерно.

1) Отсюда по теореме 26: , а поскольку каждую точку можно поместить в такой отрезок, то в каждой точке непрерывна.

2) Отсюда же по теореме 27 ряд (2) можно почленно интегрировать на отрезке , причем .

3) Покажем сначала, что при всех ряд из производных: 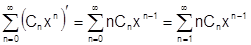(2) сходится к : .

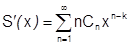Поместим х в отрезок . В данном отрезке ряд сходится к сумме 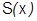. Если окажется, что ряд из производных (2) сходится на этом отрезке равномерно, то это будет означать по теореме 28, что ряд (2) сходится к .

Значит, достаточно доказать равномерную сходимость ряда (2) на отрезке . Для этого найдем мажоранту.

Поместим отрезок в отрезок . Тогда: . Но в силу сходимости ряда последовательность ограничена, то есть . Тогда , где , .

Ряд 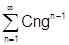и есть мажоранта, так как он сходится (можно проверить по признаку Даламбера: ). Таким образом ряд (2) на отрезке мажорируется положительным сходящимся числовым рядом, следовательно по признаку Вейерштрасса он сходится на этом отрезке равномерно (и абсолютно). Этим доказано, что ряд (2) сходится к .

Ряд (2) – это снова степенной ряд с некоторым интервалом сходимости . Как было показано, при каждом ряд (2) сходится абсолютно. Это значит, что каждое такое х входит в интервал сходимости ряда (2).

Таким образом: , т.е. при почленном дифференцировании интервал сходимости степенного ряда не уменьшается. Применяя почленное дифференцирование на интервале к степенному ряду (2) (законность почленного дифференцирования только что доказали), получим:

И вообще: ¨

Теорема 34 (о сохранении интервала сходимости). При почленном дифференцировании и почленном интегрировании степенного ряда (1) по любому отрезку интервала сходимости интервал сходимости степенного ряда сохраняется.

Доказательство: Пусть - интервал сходимости данного ряда (1), а интервал - интервал сходимости ряда из производных (2). Было доказано, что

Покажем теперь обратное включение. Берем . В этой точке ряд (2) абсолютно сходится, т.е. сходится ряд , а вместе с ним сходится и ряд (полученный почленным умножением на постоянное число ). Таким образом, сходится ряд , но , поэтому ряд (1) тем более сходится абсолютно и поэтому рассматриваемое х содержится в интервале сходимости ряда (1).

Таким образом: , т.е. . В результате , т.е. при почленном дифференцировании интервал сходимости сохраняется.

После почленного интегрирования на отрезке данного ряда (1) получим новый степенной ряд с некоторым интервалом сходимости . Если его почленно дифференцировать, то получим степенной ряд, который по доказанному имеет такой же интервал сходимости: 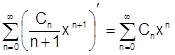, но это исходный ряд с интервалом сходимости . Следовательно в итоге интервал . Таким образом, при почленном интегрировании интервал сходимости тоже сохраняется. ¨

Замечание:при почленном дифференцировании и интегрировании сохраняется интервал сходимости, но не область сходимости, т.к. сходимость на концах интервала может меняться.

Пример:

– геометрический ряд ( , сходится 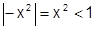) с областью сходимости 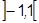. После почленного интегрирования: , при : – Лейбницевского типа, сходится; при : – сходится. Таким образом, область сходимости расширилась, теперь это .