 |
|
Задача разложения функции в степенной ряд. Единственность разложения. Формула Тейлора.
Говорят, что данная функция  разлагается в степенной ряд в окрестности данной точки
разлагается в степенной ряд в окрестности данной точки  , если в некоторой окрестности этой точки
, если в некоторой окрестности этой точки  представима в виде суммы степенного ряда по степеням
представима в виде суммы степенного ряда по степеням 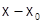 :
: 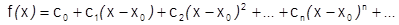 (1). Это значит, что:
(1). Это значит, что:
1. в некоторой (хотя бы малой) окрестности  ряд (1) сходится.
ряд (1) сходится.
2. сумма 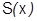 ряда (1) во всех точках этой окрестности совпадают с данной функцией:
ряда (1) во всех точках этой окрестности совпадают с данной функцией: 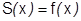 .
.
В частности, при 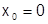 имеем:
имеем: 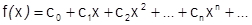 разложение
разложение  в степенной ряд в окрестности нуля по степеням
в степенной ряд в окрестности нуля по степеням  .
.
Разложение функции в степенной ряд облегчает приближенные вычисления значений функции с заданной точностью. Именно: значение  с любой заданной точностью можно заменить на частную сумму степенного ряда.
с любой заданной точностью можно заменить на частную сумму степенного ряда. 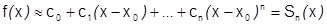 , а
, а  - это многочлен и при его вычислении используются только операции сложения, вычитания и умножения. В результате, значения самых различных функций (показательных, логарифмических, тригонометрических, …) вычисляются с помощью одних только этих операций.
- это многочлен и при его вычислении используются только операции сложения, вычитания и умножения. В результате, значения самых различных функций (показательных, логарифмических, тригонометрических, …) вычисляются с помощью одних только этих операций.
Ясно, что ряд (1) можно написать, если заданы коэффициенты 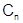 , т.е. степенной ряд вполне определяется заданием точки
, т.е. степенной ряд вполне определяется заданием точки  и набора коэффициентов
и набора коэффициентов 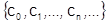 . Одна и та же функция
. Одна и та же функция  может быть разложена в окрестностях различных точек в различные степенные ряды.
может быть разложена в окрестностях различных точек в различные степенные ряды.
Например:

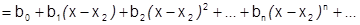
Это будут различные степенные ряды, имеющие различные наборы коэффициентов: 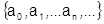 и
и 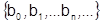 . Но оказывается, что если
. Но оказывается, что если  разлагается в степенной ряд в окрестности одной точки
разлагается в степенной ряд в окрестности одной точки  , то такой ряд единственный, т.е. каким бы способом
, то такой ряд единственный, т.е. каким бы способом  ни была разложена в степенной ряд в окрестности точки
ни была разложена в степенной ряд в окрестности точки  , получившийся ряд имеет всегда один и тот же набор коэффициентов. Это свойство называется единственностью разложения в степенной ряд.
, получившийся ряд имеет всегда один и тот же набор коэффициентов. Это свойство называется единственностью разложения в степенной ряд.
Теорема 35 (о единственности разложения функции в степенной ряд). Если функция  разлагается в окрестности точки
разлагается в окрестности точки 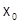 в степенной ряд, то это разложение единственно.
в степенной ряд, то это разложение единственно.
Доказательство: Пусть функция  разлагается в степенной ряд в окрестности
разлагается в степенной ряд в окрестности  точки
точки 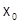 :
:  (1), тогда по теореме 33
(1), тогда по теореме 33  как сумма степенного ряда бесконечно дифференцируема на этом интервале, причем ее
как сумма степенного ряда бесконечно дифференцируема на этом интервале, причем ее  -я производная равна:
-я производная равна:


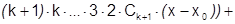
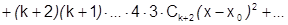
В частности, при 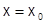 :
:
 .
.
Т.о. для всех 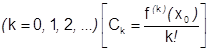 (2)
(2)
 .
.
Итак, если имеет место разложения (1), то коэффициенты  обязаны равняться числам
обязаны равняться числам 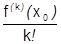 , из-за этого возможен только единственный набор таких коэффициентов.¨
, из-за этого возможен только единственный набор таких коэффициентов.¨
Если функция  бесконечно дифференцируема в какой-либо точке
бесконечно дифференцируема в какой-либо точке 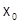 , то вычислив значения
, то вычислив значения  , можно составить набор чисел
, можно составить набор чисел 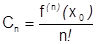 .
.
Степенной ряд по степеням 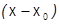 , коэффициенты которого вычислены через значения данной функции
, коэффициенты которого вычислены через значения данной функции  и ее производных в точке
и ее производных в точке 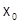 по формуле (2), т.е. ряд
по формуле (2), т.е. ряд  называется рядом Тейлора данной функции
называется рядом Тейлора данной функции  в окрестности точки
в окрестности точки 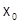 (независимо от того, будет ли
(независимо от того, будет ли  суммой этого ряда или не будет).
суммой этого ряда или не будет).
Ряд Тейлора в окрестности 0:
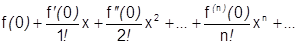 называется рядом Маклорена функции
называется рядом Маклорена функции  .
.


Если  оказывается суммой своего ряда Тейлора, то вместо знака "~" пишут "=".
оказывается суммой своего ряда Тейлора, то вместо знака "~" пишут "=".
Теперь можно сформулировать следствие из теоремы.
Следствие: Если функция  разлагается в окрестности точки
разлагается в окрестности точки 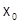 в степенной ряд, то это будет обязательно ряд Тейлора этой функции. Если функция
в степенной ряд, то это будет обязательно ряд Тейлора этой функции. Если функция 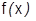 бесконечно дифференцируема в окрестности некоторой точки
бесконечно дифференцируема в окрестности некоторой точки 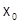 , то вычислив значения
, то вычислив значения 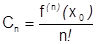 можно всегда формально написать ряд Тейлора функции
можно всегда формально написать ряд Тейлора функции  в окрестности
в окрестности 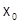 . Однако такой ряд не обязательно сходится к функции
. Однако такой ряд не обязательно сходится к функции  , породившей этот ряд. Во-первых, может оказаться, что в каких-либо точках области определения функции
, породившей этот ряд. Во-первых, может оказаться, что в каких-либо точках области определения функции  ряд Тейлора расходится. Во-вторых, если даже ряд Тейлора сходится во всей области определения функции
ряд Тейлора расходится. Во-вторых, если даже ряд Тейлора сходится во всей области определения функции  , может оказаться, что его сумма
, может оказаться, что его сумма  не совпадает с данной функцией
не совпадает с данной функцией  .
.
 Примеры:
Примеры:
1) 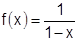 . Известно, что при
. Известно, что при  , значит, имеем разложение функции
, значит, имеем разложение функции  в окрестности точки
в окрестности точки  на интервале
на интервале  . На этом интервале
. На этом интервале 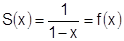 . Разложение есть. Вне интервала ряд расходится, т.е.
. Разложение есть. Вне интервала ряд расходится, т.е.  не существует, в то время, как
не существует, в то время, как  существует везде, кроме
существует везде, кроме 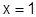 , так что вне интервала
, так что вне интервала 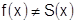 . Значит разложение существует только на
. Значит разложение существует только на 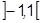 .
.
2) 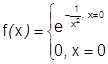
 бесконечно дифференцируема при всех
бесконечно дифференцируема при всех  , в том числе и при
, в том числе и при  .
.
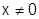 :
: 
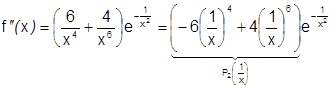
И вообще:  , где
, где 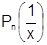 - некоторый многочлен относительно
- некоторый многочлен относительно  ,
,  . (здесь
. (здесь 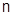 - не степень многочлена, а порядковый номер). Это можно доказать методом математической индукции.
- не степень многочлена, а порядковый номер). Это можно доказать методом математической индукции.
 :
: 
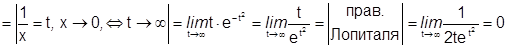
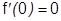 ; Докажем методом математической индукции что
; Докажем методом математической индукции что 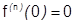 при любом
при любом 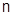 .
.
Предположим, что 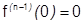 , тогда
, тогда 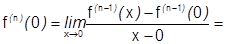


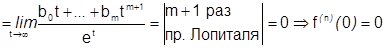 .
.
Значит при любом 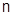
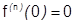 .
.
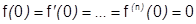 .
.
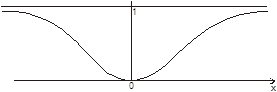
Ряд Тейлора для  в окрестности 0:
в окрестности 0: 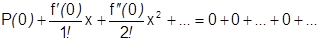 имеет сумму
имеет сумму 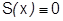 на
на 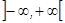 . Но
. Но 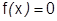 только в одной точке
только в одной точке  , следовательно
, следовательно 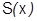 ни в какой окрестности 0 не совпадает с
ни в какой окрестности 0 не совпадает с  т.е. не смотря на то, что
т.е. не смотря на то, что  бесконечно дифференцируема в окрестности 0. Она не является суммой своего ряда Тейлора, значит не разлагается в степенной ряд в окрестности 0.
бесконечно дифференцируема в окрестности 0. Она не является суммой своего ряда Тейлора, значит не разлагается в степенной ряд в окрестности 0.
Основную роль в исследовании условий разложимостити функции в степенной ряд будет играть формула Тейлора.
Формула Тейлора.
Вопрос о разложимости в степенной ряд наиболее просто решается в случае когда  есть многочлен. Каждый многочлен разлагается в степенной ряд в окрестности любой т.
есть многочлен. Каждый многочлен разлагается в степенной ряд в окрестности любой т.  на всем интервале
на всем интервале  .
.
Пусть, например, 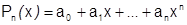 – многочлен
– многочлен 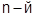 степени. При
степени. При 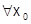 имеем
имеем 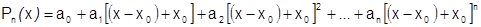 ; после возведения скобки
; после возведения скобки 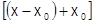 в указанные степени и приведения подобных, получим требуемое разложение:
в указанные степени и приведения подобных, получим требуемое разложение: 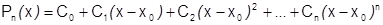 на
на 
 . Согласно теореме 35 (о единственности разложения) коэффициенты
. Согласно теореме 35 (о единственности разложения) коэффициенты  должны равняться числам
должны равняться числам 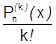 . Поэтому
. Поэтому 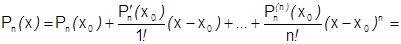
 .
.
Это разложение многочлена называется формулой Тейлора для многочлена (число членов конечно, поэтому употребляется слово «формула» вместо слова «ряд»).
Если  не многочлен, но имеет в окрестности
не многочлен, но имеет в окрестности 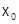 производные до
производные до  порядка, то, вычислив числа
порядка, то, вычислив числа 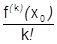 можно составить многочлен:
можно составить многочлен: 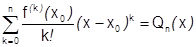 – многочлен Тейлора для
– многочлен Тейлора для  . Он отличается от
. Он отличается от  на некоторую величину
на некоторую величину 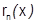 :
: 
 (1)
(1)
Это формула Тейлора для функции  в окрестности точки
в окрестности точки 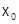 ;.
;. 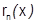 называется остаточным членом формулы Тейлора.
называется остаточным членом формулы Тейлора.
Остаточный член может иметь различный вид для различных функций, но замечательно то, что если  имеет еще и
имеет еще и 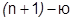 производную, то остаточный член выражается через
производную, то остаточный член выражается через 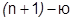 производную.
производную.
Теорема 36 (о формах остаточного члена). Если  имеет в некоторой окрестности
имеет в некоторой окрестности 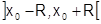 точки
точки 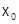 непрерывные производные до
непрерывные производные до 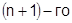 порядка включительно, то при всех
порядка включительно, то при всех 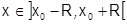 :
:
1) 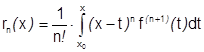 (остаточный член формулы Тейлора в интегральной форме).
(остаточный член формулы Тейлора в интегральной форме).
2) 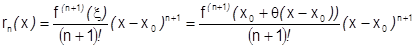 , где
, где 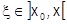 ,
, 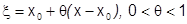 (в форме Лагранжа).
(в форме Лагранжа).
3)  , где
, где 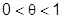 (в форме Коши).
(в форме Коши).
Доказательство:
1) 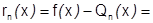
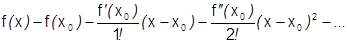
 .
.
Поскольку на интервале  существуют непрерывные производные:
существуют непрерывные производные: 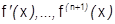 , то
, то 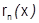 тоже имеет непрерывные производные:
тоже имеет непрерывные производные: 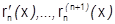 (т.к. выражается через
(т.к. выражается через 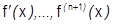 ).
).

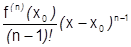 ;
;
( 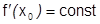 )
)
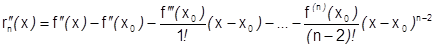 ;
;
…
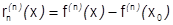 ;
;
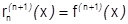 .
.
В частности:  .
.
С учетом этих равенств получим: 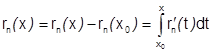 (все
(все 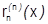 на отрезке
на отрезке  непрерывны, поэтому все интегралы с их участием существуют)=
непрерывны, поэтому все интегралы с их участием существуют)= 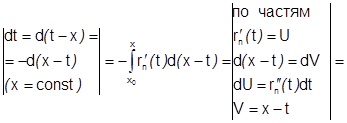

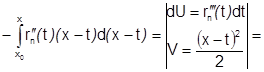
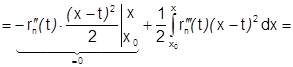
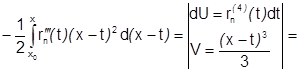
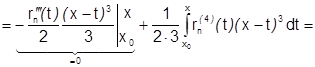

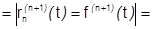
 и формула (1) доказана.
и формула (1) доказана.
Формулы (2) и (3) выведем из (1), используя обобщенную теорему о среднем для определенного интеграла.
2) Пусть 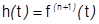 , по условию
, по условию 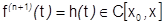 .
.
Тогда 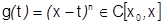 , кроме того
, кроме того 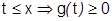 на отрезке
на отрезке  . Поэтому
. Поэтому 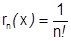
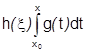 , где
, где 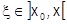 .
. 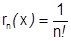

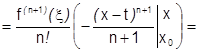
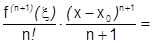
 . Здесь
. Здесь 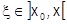 , обозначим
, обозначим 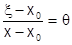 , поскольку всегда
, поскольку всегда 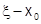 и
и 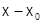 - одного знака, то отношение
- одного знака, то отношение 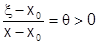 . Кроме того
. Кроме того 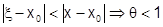 , т.е.
, т.е. 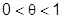 и можно взять отсюда
и можно взять отсюда 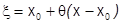 . Подставляя, получим:
. Подставляя, получим:
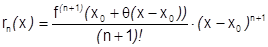 . Формула 2) доказана.
. Формула 2) доказана.
3) Пусть 
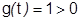 (тоже сохраняет знак), тогда
(тоже сохраняет знак), тогда 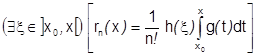 .
.
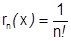
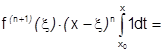
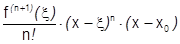 . Заметим:
. Заметим: 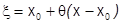 ,
, 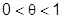 ;
; 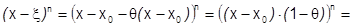
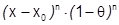 . Итак:
. Итак:
 – формула 3) доказана.¨
– формула 3) доказана.¨