 |
|
Условия разложимости функции в степенной ряд.
Согласно теореме 33, сумма степенного ряда по степеням 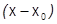 должна быть бесконечно дифференцируемой на некотором интервале
должна быть бесконечно дифференцируемой на некотором интервале 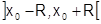 . Поэтому разлагаться в степенной ряд в окрестности
. Поэтому разлагаться в степенной ряд в окрестности 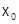 может только такая функция, которая бесконечно дифференцируема в этой окрестности. Но, как показывает пример 2 (см. 2.7), бесконечная дифференцируемость не достаточна для того, чтобы функция разлагалась в степенной ряд.
может только такая функция, которая бесконечно дифференцируема в этой окрестности. Но, как показывает пример 2 (см. 2.7), бесконечная дифференцируемость не достаточна для того, чтобы функция разлагалась в степенной ряд.
Теорема 37 (критерий разложимости в степенной ряд).Функция  , бесконечно дифференцируемая в окрестности точки
, бесконечно дифференцируемая в окрестности точки 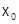 , разлагается в степенной ряд в этой окрестности тогда и только тогда, когда остаточный член формулы Тейлора функции
, разлагается в степенной ряд в этой окрестности тогда и только тогда, когда остаточный член формулы Тейлора функции  во всех точках окрестности стремится к 0 при
во всех точках окрестности стремится к 0 при 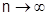 .
.
Доказательство: заметим, что в формуле Тейлора  многочлен
многочлен  есть n-я частная сумма
есть n-я частная сумма  ряда
ряда 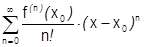 , поэтому [
, поэтому [  разлагается в степенной ряд в окрестности
разлагается в степенной ряд в окрестности 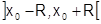 :
: 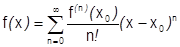 ]
] 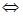
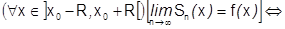
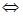
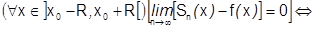
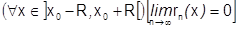 , что и требовалось доказать.¨
, что и требовалось доказать.¨
Таким образом, если  имеет в окрестности точки
имеет в окрестности точки 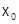 производные всех порядков то для разложения ее в степенной ряд нужно:
производные всех порядков то для разложения ее в степенной ряд нужно:
1) формально составить формальный ряд Тейлора,
2) найти область сходимости этого ряда,
3) выбрать из этой области те точки 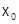 , в которых
, в которых 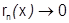 при
при 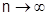 . Именно в этих точках функция.
. Именно в этих точках функция.
 равна сумме своего степенного ряда (остаточный член формулы Тейлора
равна сумме своего степенного ряда (остаточный член формулы Тейлора 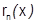 можно брать в форме Л. или Коши).
можно брать в форме Л. или Коши).
Иногда исследование остаточного члена трудно, в этих случаях может быть полезной следующая теорема:
Теорема 38 (достаточное условие разложимости в степенной ряда). Если  бесконечно дифференцируема в окрестности
бесконечно дифференцируема в окрестности 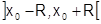 точки
точки 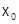 , причем производные всех порядков в этой окрестности ограничены одним и тем же числом:
, причем производные всех порядков в этой окрестности ограничены одним и тем же числом:  , (
, ( 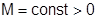 ) то
) то  разлагается в степенной ряд в окрестности
разлагается в степенной ряд в окрестности 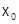 .
.
Доказательство:достаточно показать, что 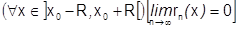 .
.
Возьмем 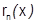 в форме Лагранжа:
в форме Лагранжа: 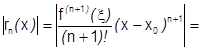
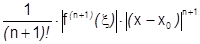 , где
, где 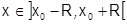 , Поскольку
, Поскольку 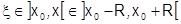 то
то 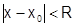 .
.
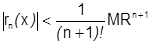 .
.
Но  есть общий член сходящегося ряда (пр. Даламбера
есть общий член сходящегося ряда (пр. Даламбера 
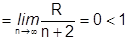 ), поэтому он стремится к 0:
), поэтому он стремится к 0: 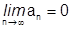 , тогда тем более
, тогда тем более 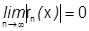
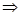
 .¨
.¨
2.10 Разложение некоторых элементарных
функций в степенной ряд.
Рассмотрим разложение элементарных функций в степенной ряд в окрестности 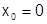 , т.е. ряд Маклорена:
, т.е. ряд Маклорена: 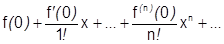 Отметим, что формула Тейлора в окрестности
Отметим, что формула Тейлора в окрестности  :
:  называется формулой Маклорена.
называется формулой Маклорена.
Остаточный член формулы Маклорена имеет вид:
а)  ,
,  ;
; 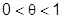 ; в форме Лагранжа и
; в форме Лагранжа и
б)  ,
, 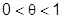 ; в форме Коши.
; в форме Коши.
1) Логарифмический ряд: 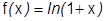 . Бесконечно дифференцируема при
. Бесконечно дифференцируема при 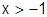 (
( 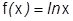 не берем, т.к. при
не берем, т.к. при 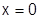 не существует).
не существует).
 .
.


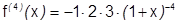
…
 . (методом математической индукции при
. (методом математической индукции при 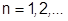 )
)
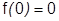 ,
, 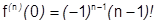
1) Составим ряд Маклорена:
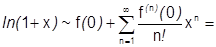
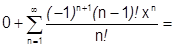
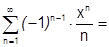
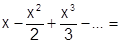
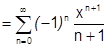 .
.
2) Найдем области сходимости: 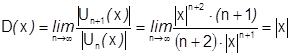 .
.
Ряд абсолютно сходится при 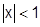 , расходится при
, расходится при  .
.
Исследуем на концах:
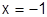 :
: 
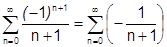 расходится как отрицательный гармонический ряд.
расходится как отрицательный гармонический ряд.
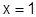 :
: 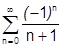 – сходится, т.к. лейбницевского типа, но не абсолютно.
– сходится, т.к. лейбницевского типа, но не абсолютно.
Область сходимости: 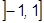 .
.
3) Исследуем поведение 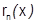 в этой области. Возьмем
в этой области. Возьмем 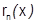 в формуле Лагранжа
в формуле Лагранжа 
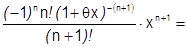

(т.к 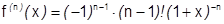 ),
),

а) при 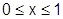 получается простая оценка:
получается простая оценка: 
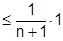 , отсюда:
, отсюда: 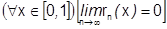 .
.
б) При 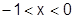 оценка затрудняется, поэтому возьмем теперь
оценка затрудняется, поэтому возьмем теперь 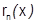 в форме Коши:
в форме Коши: 
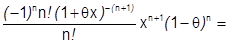
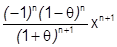 .
.
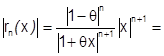
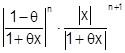 .
.
1-й множитель: 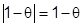 , т.к.
, т.к. 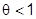 .
.
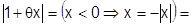
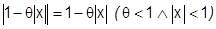 .
.
Кроме того, 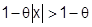 , т.к.
, т.к.  . Следовательно,
. Следовательно, 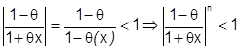 .
.
2-й множитель: 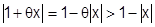 т.к.
т.к. 
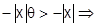
 . Следовательно
. Следовательно 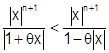 .
.
Т.о.  .
. 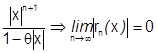 , т.к.
, т.к. 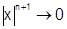 из-за
из-за  . Т.о.
. Т.о. 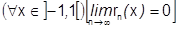 . Следовательно
. Следовательно  разлагается в ряд Маклорена на промежутке
разлагается в ряд Маклорена на промежутке 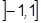 :
: 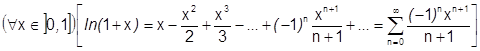 .
.
Пример: 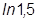 можно вычислить без таблиц.
можно вычислить без таблиц.
2) Биноминальный ряд.  ,
, 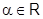 . Бесконечно дифференцируема в области определения. Аналогично предыдущему найдем:
. Бесконечно дифференцируема в области определения. Аналогично предыдущему найдем: 
 .
.
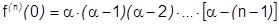 :
: 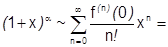
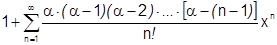 . Пользуясь признаком Даламбера, можно найти интеграл сходимости
. Пользуясь признаком Даламбера, можно найти интеграл сходимости  . Можно доказать, что
. Можно доказать, что  (доказательство сложное).
(доказательство сложное).
Следовательно  разлагается на интервале
разлагается на интервале  :
: 
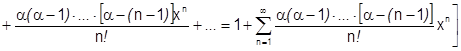
Замечание: если 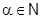 , то имеем обычный бином Ньютона:
, то имеем обычный бином Ньютона: 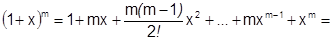
 причем это разложение верно на всем интервале
причем это разложение верно на всем интервале 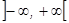 .
.
3) Ряд экспоненты. 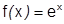 .
.
Функция бесконечно дифференцируема на всем множестве  , причем
, причем  и если взять конечный интервал
и если взять конечный интервал 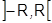 , то в силу
, то в силу  , т.е. для
, т.е. для  .
.
Это означает, что производные всех порядков на 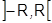 ограничены постоянной
ограничены постоянной 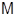 , поэтому
, поэтому  разлагается согласно теореме 38 в ряд Маклорена на этом интервале. В силу произв-ти
разлагается согласно теореме 38 в ряд Маклорена на этом интервале. В силу произв-ти 
 разлагается на всем интервале
разлагается на всем интервале 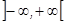 .
.
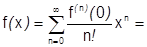
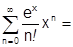

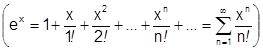
Можно вычислить число  с любой точностью.
с любой точностью.
4)  .
.
Бесконечно дифференцируема: 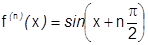 .
. 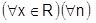
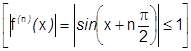
 по теореме 38 синус разлагается на всей числовой оси.
по теореме 38 синус разлагается на всей числовой оси.
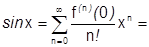
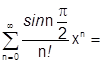


 .
.
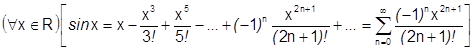 .
.
5) 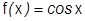 .
.
Можно поступить как с синусом, но мы воспользуемся известным рядом для синуса.
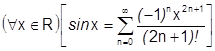
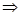
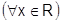
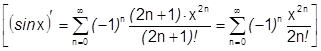
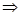
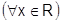
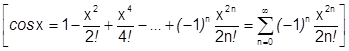 .
.
Согласно теореме о единственности разложения этот ряд и есть ряд Маклорена.
6) Ряд арктангенса: 
Воспользуемся равенством 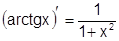 .
.
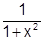 можно рассматривать как сумму геометрического ряда, у которого
можно рассматривать как сумму геометрического ряда, у которого  .
.
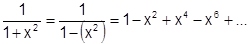 при
при 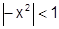 ,
, 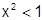 ,
, 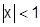 .
.
Поэтому: 
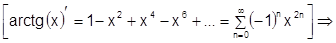
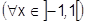
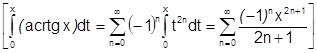
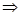
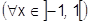
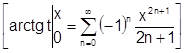 .
.
Можно доказать, что равенство верно при  , так что
, так что 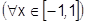
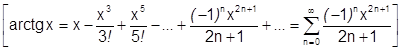 . По теореме о единственности разложения этот ряд и степенной ряд Маклорена.
. По теореме о единственности разложения этот ряд и степенной ряд Маклорена.
Пример: 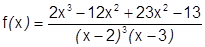
Разложить в окрестности 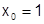 (т.е. по степеням
(т.е. по степеням 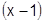 )
) 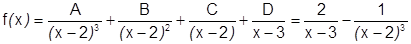
Примем 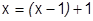 , тогда:
, тогда: 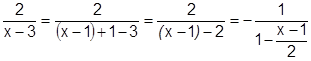 . При
. При 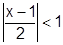 , т.е.
, т.е. 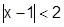 , имеем сумму геометрического ряда с
, имеем сумму геометрического ряда с 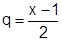 :
:
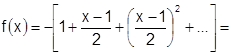
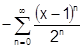 . С другой стороны
. С другой стороны 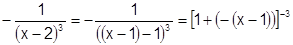 .
.
Если 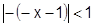 , т.е.
, т.е. 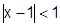 , то имеет сумму биномиального ряда:
, то имеет сумму биномиального ряда:
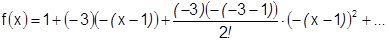
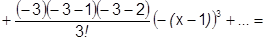
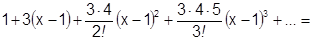 =
= 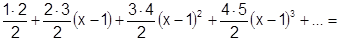
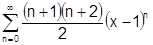 .
.
В итоге: при  имеют место оба разложения одновременно и
имеют место оба разложения одновременно и 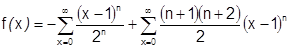 Итак,
Итак, 
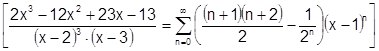 .
.
В силу единственности разложения это и есть ряд Маклорена.