 |
|
ДИНАМИКА МАТЕРИАЛЬНОЙТОЧКИ
Ø Импульс 
(количество движения) – это произведение массы т тела на его скорость υ:
.
Ø Закон сохранения импульса для замкнутой системы: импульс замкнутой системы не изменяется во времени:
,
где п – число материальных точек (или тел), входящих в систему.
Ø Первый закон Ньютона:Всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её (его) изменить это состояние.
Ø Второй закон Ньютона (основное уравнение динамики материальной точки): скорость изменения импульса тела равна действующей на него силе:
или 
это же уравнение в проекциях на касательную и нормаль к траектории точки:
и 
.
Ø Третий закон Ньютона: силы, с которыми действуют друг на друга два тела, равны по величине и противоположны по направлению:
.
Ø Основное уравнение динамики поступательного движения системы тел:
,
где 
ускорение центра инерции системы; 
– общая масса системы из п материальных точек.
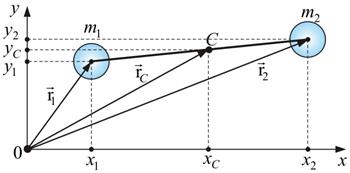
Ø Центр масс системы материальных точек:
.
Ø Импульс системы тел:
,
где 
скорость центра инерции системы.
Ø Теорема о движении центра масс:
.
СИЛЫ В МЕХАНИКЕ
Ø 
Связь веса тела 
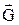с силой тяжести и реакцией опоры 
: 
,
ускорение свободного падения.
Ø Соотношение между весом, силой тяжести и ускорением:
.
Ø Сила трения скольжения:
где 
– коэффициент трения скольжения; N – сила нормального давления.
Ø Сила трения качения:
,
где 
– коэффициент трения качения; r – радиус катящегося тела.
Ø 
Основные соотношения для тела на наклонной плоскости:
· сила трения: 
;
· равнодействующая сила: 
;
· скатывающая сила: 
;
· ускорение: 
.
Ø 
Центростремительная сила – сила инерции второго рода, приложенная к вращающемуся телу и направленная по радиусу к центру вращения:
,
где 
центростремительное ускорение.
Ø Центробежная сила – сила инерции первого рода, приложенная к связи и направленная по радиусу от центра вращения:
,
где 
центробежное ускорение.
Ø Сила Кориолиса:
,
где 
угловая скорость вращения.
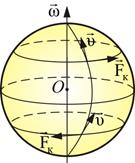
Ø Закон Гука для пружины: удлинение пружины х пропорционально силе упругости или внешней силе:
,
где k – жесткость пружины.
Ø Потенциальная энергия упругой пружины:
.
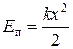Ø Работа, совершённая пружиной:
.
Ø 
Напряжение– мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий:
,
где 
площадь поперечного сечения стержня, d – его диаметр.
Ø Приращение длины стержня 
пропорционально напряжению:
.
Ø Относительное продольное растяжение (сжатие):
.
Ø Относительное поперечное растяжение (сжатие):
,
где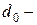 
начальный поперечный размер стержня.
Ø Коэффициент Пуассона – отношение относительного поперечного растяжения стержня 
к относительному продольному растяжению 
:
.
Ø Модуль Юнга – величина, характеризующая упругие свойства материала стержня:
Ø Закон Гука для стержня: относительное приращение длины стержня прямо пропорционально напряжению и обратно пропорционально модулю Юнга:
.
Ø Объемная плотность потенциальной энергии:
.
Ø Относительный сдвиг:
,
где 
абсолютный сдвиг.
Ø Модуль сдвига G – величина, зависящая от свойств материала и равная такому тангенциальному напряжению, при котором 
(если бы столь огромные упругие силы были возможны).
.
Ø 
Тангенциальное упругое напряжение:
.
Ø Закон Гука для сдвига:
или 
.
Ø Удельная потенциальная энергия тела при сдвиге:
.