Главная | Обратная связь

ЭНЕРГИЯ. РАБОТА. ЗАКОНЫ СОХРАНЕНИЯ

Ø Кинетическая энергия – функция состояния системы, определяемая только скоростью её движения:

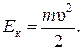
Ø Связь кинетической энергии с импульсом:

.

Ø Изменение кинетической энергии равно работе внешних сил:

.

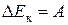Ø Работа переменной силы на участке траектории 1 – 2:

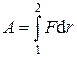или .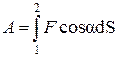

Ø Мгновенная мощностьравна работе, совершаемой в единицу времени:

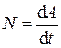или .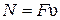

Ø Средняя мощность за промежуток времени :

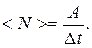
Ø Работа консервативных силравна изменению потенциальной энергии:

.

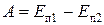Ø Теорема о циркуляции вектора : если циркуляция какого-либо вектора силы равна нулю, то эта сила консервативна.

Работа консервативных сил вдоль замкнутого контура L равна нулю:

.

Ø Гравитационное взаимодействие между массами m и M:

.

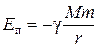Ø Потенциальная энергия сжатой пружины:

.

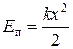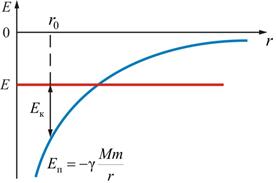
Ø Полная механическая энергия системыравна сумме кинетической и потенциально энергий:

.

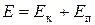Ø Потенциальная энергия тела на высоте h над землей:

.

Ø Закон сохранения механической энергии(для замкнутой системы): полная механическая энергия консервативной системы материальных точек остается постоянной:

.

Ø Связь между потенциальной энергией и силой:

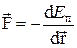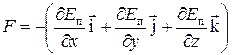или или

Ø Закон сохранения механической энергии и импульса при абсолютно упругом центральном ударе:

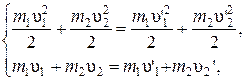
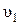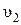где m₁ и m₂ – массы тел; и – скорости тел до удара.

Ø Скорости телпосле абсолютно упругого удара:

.

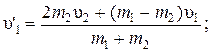
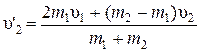Ø Скорость движения тел после абсолютно неупругого центра­льного удара:

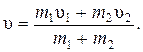
Ø Закон сохранения импульса при движении ракеты:

,

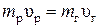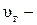где и – масса и скорость ракеты; и масса и скорость выбрасываемых газов.

Ø Уравнение Мещерского для ракеты:

.

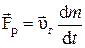Ø Формула Циолковскогодля определения скорости ракеты (характеристическая скорость):

,

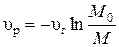где М₀ и М – начальная и конечная массы ракеты.

5. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Ø Момент силы относительно неподвижной точки:

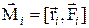или .

где r– радиус-вектор, проведенный из этой точки в точку прило­жения силы F; l – плечо силы F.

Ø Момент импульса относительно неподвижной точки:

,

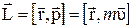где 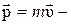импульс тела.

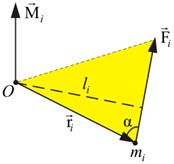
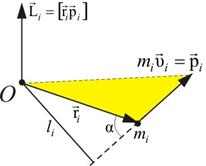
Ø Основной закон динамики вращательного движения относительно точки:

.

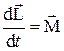Ø 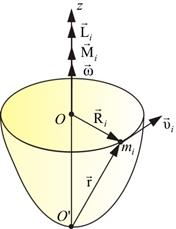Момент инерции точки, находящейся на расстоянии 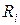от оси вращения:

.

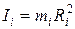Ø Момент импульса (момент количества движения) твердого тела относительно оси вращения:

,

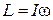где 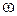– угловая скорость вращения тела.

Ø Уравнение динамики вращательного движения твердого тела:

.

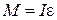Ø Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени:

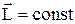или .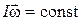

 

 

Ø Момент инерции системы (тела):

где R – расстояние материальной точки массой до оси вращения.

· Для сплошного однородного тела:

,

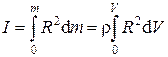где ρ – плотность тела; V – объем тела.

Ø Теорема Штейнера: момент инерции тела I относительно любой оси вращения равен моменту его инерции I_с относительно параллельной оси, проходящей через центр масс С тела, плюс произведение массы тела на квадрат расстояния между осями:

.

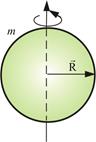
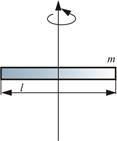
Ø Моменты инерции тел правильной геометрической формы:

Шар ; 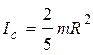Сфера	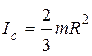Диск ; Обруч	Стержень ;

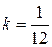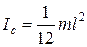
Ø Кинетическая энергия тела, вращающегося с угловой скоростью ω вокруг неподвижной оси z,

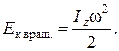
Ø Полная кинетическая энергия тела, катящегося по плоскости без скольжения:

.

 

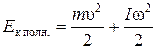Ø 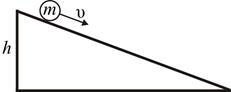Закон сохранения энергии для тела катящегося с высоты h:

.
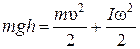