Главная | Обратная связь

Две формы записи линейных дифференциальных уравнений

Пусть дано уравнение

a₀ÿ + a₁ + a₂y = b₀x + b₁ + cf, (1.2.1)

.

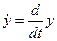
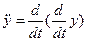Введём обозначение оператора дифференцирования 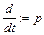. Тогда

=pу, =p²y, =p³y. (1.2.2)

Найдем оператор интегрирования или = х, или py = x, откуда .

— оператор интегрирования.

Запишем уравнение (1) в операторном виде

(a₀p²+a₁p+a₂)y=(b₀+b₁p)+cf. (1.2.3)

Первая форма записи

В первой форме выходная переменная записывается в одной части уравнения, а входные переменные в другой части уравнения, причём коэффициент при самой выходной переменной ( у ) должен быть равен единице. Введем обозначения

.

Тогда уравнение (1) и (3) перепишутся в виде

T₁² +T₂ +y=m₀x+m₁x+nf, (1.2.4)

(T₁²p²+T₂p+1)y=(m₀+m₁p)x+nf. (1.2.5)

D(p)

 

В первой форме записи коэффициенты Т₁, Т₂ при любых физических переменных у имеют размерность времени. Это обеспечивает универсальность данной формы записи.

Коэффициенты m₀ , m_1, n называют коэффициентами передачи. Если коэффициенты m_{0 ,} n безразмерные, то они называются коэффициентами усиления. Коэффициенты Т₁, Т₂ называются постоянными времени. Коэффициент Т₁, стоящий при старшей производной, характеризует инерционность звена, чем больше Т₁ , тем более инерционные процессы.

Вторая форма записи

Решим уравнение (5) относительно выходной переменной у

y=y₁+y₂=W₁(p)x+W₂(p)f, (1.2.6)

где

(1.2.7)

y₁=W₁(p)x , y₂=W₂(p)f , (1.2.8)

(1.2.9)

W₁,W₂ — передаточные функции.

Передаточная функция равна отношению выходного сигнала к входному. Если использовать преобразование Лапласа, то передаточная функция равна отношению преобразованного по Лапласу выходного сигнала к преобразованному по Лапласу входному сигналу при нулевых начальных условиях. Передаточная функция показывает какие математические операции надо проделать с входным сигналом, чтобы получить выходной сигнал. Уравнение (6) представляет собой вторую форму записи дифференциального уравнения (1), то есть запись через передаточные функции.

Вторая форма записи позволяет представить дифференциальное уравнение и системы дифференциальных уравнений в графическом виде. Для этого вводятся следующие графические обозначения:

 

Сумматор Компаратор

Рисунок 1.2.1.

Уравнение (6) в графическом виде будет выглядеть так:

 

 

Рисунок 1.2.2. Структурная схема уравнения (1).