Главная | Обратная связь

Частотные критерии устойчивости

Будем рассматривать следующие критерии:

— критерий Михайлова;

— критерий Найквиста;

— логарифмический критерий Найквиста.

1.9.3.1 Критерий Михайлова.Для его применения необходимо иметь характеристический полином

D(p)=a₀pⁿ+a₁p^n-1+…+a_n-1p+a_n. (1.9.3.1)

Подставим в (1) p=jw, где j= ; w — частота, которая меняется в диапазоне от 0 до ∞. В результате получим комплексный полином

D(jw)=X(w)+jY(w), (1.9.3.2)

где X(w) — действительная часть, а Y(w) — коэффициент при мнимой части.

X(w)=a_n-a_n-2w²+a_n-4w⁴-a_n-6w⁶+…, (1.9.3.3)

Y(w)=a_n-1w-a_n-3w³+a_n-5w⁵-a_n-7w⁷+…,

или

Y(w)=w·(a_n-1-a_n-3w²+a_n-5w⁴-a_n-7w⁶+…). (1.9.3.4)

Критерий Михайлова является графическим критерием. Для его применения на комплексной плоскости строится годограф (траектория конца вектора) Михайлова. На рис. 1.9.6 показаны годографы (траектории конца вектора) Михайлова для систем различных порядков n, соответствующие асимптотической устойчивости систем.

 

Рисунок 1.9.6 Годографы Михайлова для систем различных порядков.

 

Для того чтобы система была асимптотически устойчивой, необходимо и достаточно, чтобы при изменении частоты w от 0 до ∞ годограф Михайлова охватывал начало координат, проходя последовательно столько квадрантов против часовой стрелки, каков порядок системы.

Если годограф Михайлова будет проходить через начало координат, то система будет находиться на границе устойчивости (рисунок 1.9.7).

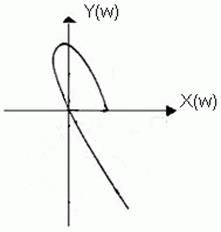
Рисунок 1.9.7. Рисунок 1.9.8.

Если годограф Михайлова не охватывает начало координат, то САУ будет неустойчивой (рис. 1.9.8).

Из критерия Михайлова вытекает критерий Эрмита-Билера. Как следует из рисунка 1.9.6, при асимптотической устойчивости корни полиномов X(w)=0, Y(w)=0 чередуются.

Критерий Эрмита-Билера. Для того чтобы система была асимптотически устойчивой, необходимо и достаточно, чтобы корни полиномов (3) и (4) были действительными положительными и чередовались между собой, начиная с корня w=0 для полинома (4).

1.9.3.2 Критерий Найквиста.Этот критерий позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутой системы. Для применения этого критерия система приводится к виду с единичной обратной связью, показанному на рис. 1.9.9.

 

 

─

Рисунок 1.9.9.

На рис. 1.9.9 g — задающее воздействие, равное желаемому значению выходной переменной у; x – ошибка системы; W(p) – передаточная функция разомкнутой системы представленная в виде

(1.9.3.5)

При таком представлении передаточной функции k – коэффициент передачи разомкнутой цепи, n — степень астатизма.

При n=0 система называется статической, при n=1,2,… система называется астатической первого, второго, … порядков.

Для реальных систем имеет место соотношение

n+q>m. (1.9.3.6)

Передаточная функция замкнутой САУ имеет вид

. (1.9.3.7)

Для получения характеристического уравнения необходимо положить

1+W(p)=0. (1.9.3.8)

Подставим в уравнение (8) p=jw

где, как и ранее j= , w — частота. Получим

W(jw)=-1. (1.9.3.9)

Т.е. значение w, при котором выполняется условие (9), является корнем характеристического уравнения (4), т.е. p=jω, что соответствует границе устойчивости. Но W(jw) — представляет собой АФЧХ разомкнутой системы.

Таким образом, если АФЧХ разомкнутой системы при изменении частоты от 0 до ∞ будет проходить через точку (-1,j0), то система будет находится на границе устойчивости.

Будем рассматривать две ситуации:

а) система в разомкнутом состоянии устойчива (асимптотически устойчива или находится на границе устойчивости);

б) система в разомкнутом состоянии неустойчива.

Случай а):

Критерий Найквиста. Для того чтобы замкнутая система была асимптотически устойчива, необходимо и достаточно, чтобы при изменении частоты от 0 до бесконечности АФЧХ разомкнутой системы не огибала точку с координатами (-1, j0).

Если АФЧХ будет проходить через эту точку, то замкнутая САУ будет находиться на границе устойчивости.

Если АФЧХ будет огибать точку (-1, j0), то замкнутая САУ будет неустойчивой.

Годографы Найквиста для статической системы (n=0) представлены на рис. 1.9.10, а для астатической системы (n=1) представлены на рис. 1.9.11.

 

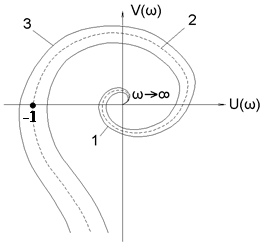
Рисунок 1.9.10. Рисунок 1.9.11.

На рисунках 1.9.10, 1.9.11: W(jw)=U(w)+jV(w),

1 — устойчивая замкнутая САУ,

2 — граница устойчивости САУ,

3 — неустойчивая САУ.

Рассмотрим случай астатической системы первого порядка. В этом случае годографы Найквиста выглядят так:

Случай б): система в разомкнутом состоянии неустойчива. Тогда критерий Найквиста выглядит так:

Для того чтобы система неустойчивая в разомкнутом состоянии была асимптотически устойчива в замкнутом состоянии, необходимо и достаточно, чтобы при изменении частоты от минус бесконечности до плюс бесконечности АФЧХ разомкнутой системы охватывала точку с координатами (-1, j0) столько раз, сколько корней в правой полуплоскости содержит знаменатель передаточной функции разомкнутой системы. При этом необходимо, чтобы при изменении частоты от минус бесконечности до плюс бесконечности конец вектора W(jw) поворачивался вокруг точки (-1, j0) против часовой стрелки на угол m·2p, где m — количество неустойчивых корней в знаменателе передаточной функции разомкнутой системы.

При m=1 (одном корне) годограф Найквиста представлен на рисунке 1.9.12.

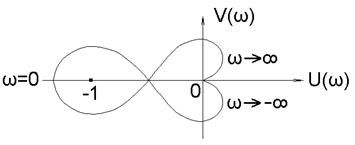
Рисунок 1.9.12.

1.9.3.3 Применение критерия Найквиста к системам с чистым запаздыванием.Рассмотрим структурную схему САУ, представленную на рис 1.9.13,

 

─

Рисунок 1.9.13

где W₁(p) — передаточная функция разомкнутой системы без учёта чистого запаздывания.

W₂(p)=e^-pt, передаточная функция чистого запаздывания (t – величина чистого запаздывания).

На рис. 1.9.14 продемонстрировано соотношение между входным ( ) и выходным сигналами звена чистого запаздывания.

 

 

Рисунок 1.9.14.

Пусть система без учёта чистого запаздывания является асимптотически устойчивой с годографом Найквиста, представленным на рис.1.9.15.

Задача: найти значение чистого запаздывания, при котором система выходит на границу устойчивости. Это значение называется критическим запаздыванием t_кр

Передаточная функция разомкнутой САУ

W(p)=W₁(p)·W₂(p),

АФЧХ разомкнутой системы

. (1.9.3.10)

На основании (10) можно заключить, что АЧХ в системе без учёта чистого запаздывания и с учётом чистого запаздывания совпадают, а ФЧХ полной системы имеет сдвиг по фазе на величину -wt по отношению к идеальной системе. Очевидно, что при возрастании w угол поворота wt увеличивается. Пусть система без запаздывания асимптотически устойчива и в разомкнутом и в замкнутом состояниях. Это означает, что АФЧХ не охватывает точку (-1, j0). Будем увеличивать запаздывание t и следить за деформацией годографа W(jw). При t=t_кр годограф пройдет через точку (-1, j0) и, следовательно, система окажется на границе устойчивости. Данная ситуация отражена на рис. 1.9.15. На рисунке 1- АФЧХ W₁(jw), 2-полуокружность единичного радиуса, – точка пересечения кривой с полуокружностью 2. Поскольку в этой

Рисунок 1.9.15.

 

точке , то в этой точке . Подчеркнем, что частоты среза в системах с чистым запаздыванием и без него совпадают. На основании рис.15 можно записать

j=w_срt.

Угол j можно замерить на рисунке 15, тогда

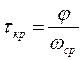. (1.9.3.11)

1.9.3.4 Логарифмический критерий Найквиста.Это тот же критерий Найквиста, но сформулированный на языке логарифмических характеристик. Для наглядности рассмотрим специфическое взаимное расположение ЛАЧХ и ЛФЧХ, где угол ФЧХ расположен на горизонтали, соответствующей 0 дБ, а положительная полуось ФЧХ направлена вниз. Описанная ситуация отражена на рис. 1.9.16.

Критерий. Для того чтобы замкнутая система была асимптотически устойчивой, необходимо и достаточно, чтобы при заданном взаимном расположении систем координат ЛАЧХ и ЛФЧХ и при изменении частоты от 0 до бесконечности ЛФЧХ должна огибать точку среза снизу (кривая 1).

 

Рисунок 1.9.16

Для того чтобы замкнутая САУ находилась на границе устойчивости, ЛФЧХ должна проходить через точку среза (кривая 2).

Для того чтобы замкнутая САУ была неустойчивой, достаточно чтобы ЛФЧХ огибала точку среза сверху (кривая 3).

Содержание рис.16 называется диаграммой Боде. По этой диаграмме и выражению (11) можно найти критическое запаздывание.