Главная | Обратная связь

Показатели точности САУ

Пусть передаточная функция объекта управления по управляющему воздействию имеет вид

(1.10.1.4)

(статический объект управления).

Пусть также W_н(p) имеет структуру, аналогичную (4), но возможно с другими степенями полиномов т.е.

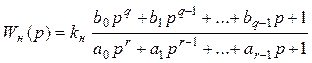. (1.10.1.5)

В общем случае в установившемся режиме , но 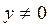. Тогда в операторном виде можно записать

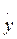= py Þ ^y¹0p=0,

т.е. для получения ошибки в установившемся режиме нужно в выражении (2) положить p=0.

Рассмотрим случай когда k₂=0 (П- или ПД-регулятор) и найдём установившуюся ошибку. С учетом того, что

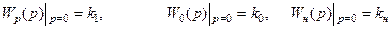, (1.10.1.6)

из (2) при 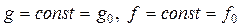получим

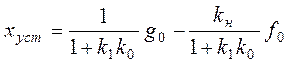. (1.10.1.7)

Система, которая при постоянных входных сигналах имеет отличную от нуля ошибку, называется статической системой. Показателем точности статической системы является её статизм

. (1.10.1..8)

Пусть теперь k₂¹0 найдём установившуюся ошибку, устремив p к 0.

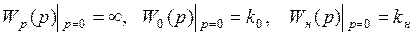(1.10.1.9)

Подставим (9) в (2). Получим

.

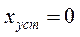Система, которая при постоянных входных воздействиях имеет нулевую постоянную ошибку, называется астатической системой.

Пусть теперь входные воздействия линейно зависят от времени, т.е.

(1.10.1.10)

Запишем (10) в операторном виде. Для этого представим время t в операторном виде

.

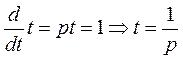Тогда из (10) получим

(1.10.1.11)

Подставим (11), (3), (4), (5) в (2) и положим, что k₂=0. Тогда 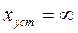, т.е. система оказывается неработоспособной.

Пусть теперь k₂¹0. При очень маленьких р будем иметь

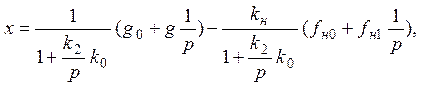
откуда

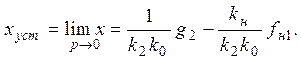(1.10.1.12)

Добавление интеграла в закон управления делает систему астатической I–го порядка. Показателем точности астатической системы I–го порядка является добротность по скорости

. (1.10.1.13)

Для обнуления ошибки (12) надо в закон управления (1) добавить двойной интеграл. Получится астатическая система второго порядка.

В астатической системе второго порядка показателем точности является добротность по ускорению. Необходимо заметить, что дифференциальная составляющая закона управления не влияет на установившуюся ошибку. Поскольку в знаменателях выражения (2) присутствует произведение W_pW₀, поэтому безразлично за счёт какого из этих сомножителей формируется астатизм системы.

О статизме и астатизме системы можно судить по передаточной функции разомкнутой системы

W(p) = W_p(p)·W₀(p).

Если в знаменателе передаточной функции можно выделить множитель p^υ, т.е. представить

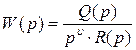, (1.10.1.14)

где Q(p) и R(p) полиномы (многочлены) от р, то при υ = 0 замкнутая система будет статической, при υ = 1 (2) – астатической первого (второго) порядка. В соответствии с (1.8.6) и (14) передаточная функция замкнутой системы по ошибке

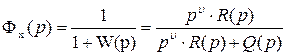. (1.10.1.15)

Из (15) следует, что о статизме и астатизме системы можно судить по числителю передаточной функции Ф_х(р).

1.10.2 Определение показателей качества в переходных процессах.Это прямой метод определения показателей качества. Рассматривается система со структурной схемой, приведенной к единичной обратной связи, представленная на рис. 1.10.2.

x

─

 

Рисунок 1.10.2 Структурнай схема

Рассмотрим переходный процесс, возникающий на выходе системы при подаче на её вход ступенчатого воздействия.

 

 

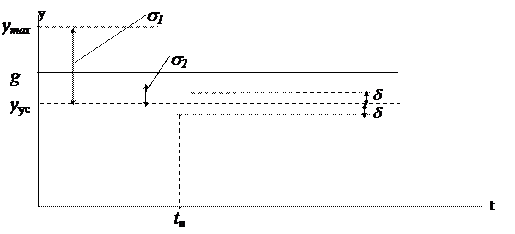Рисунок 1.10.3. Переходной процесс.

Величина s₁ называется абсолютным перерегулированием.

Показателем качества является относительное перерегулирование.

. (1.10.2.1)

Система считается хорошей, когда s лежит в пределах от 0,1 до 0,3.

Другим показателем качества является затухание за период

. (1.10.2.2)

Система считается хорошей, когда x лежит в пределах от 0,9 до 0,98.

Переходный процесс считается окончившимся с того момента, когда колебания окончательно войдут в зону ±d относительно установившегося значения.

Для точных общепромышленных систем полагают, что d/у_уст=0,01, а для грубых систем d/у_уст=0,05.

Третьим показателем качества является время переходного процесса t_п. Время переходного процесса равно промежутку времени от начала переходного процесса до его окончания.

Колебательность — это количество перерегулирований за время переходного процесса. На рисунке 3 колебательность равна 2.

По переходному процессу для статической системы можно определить её статизм(см. 1.10.1.8).

(1.10.2.3)

 

1.10.3 Определение показателей качества по корням характеристического уравнения.(См. раздел 1.9.1 «Корневые критерии устойчивости») Корни характеристического уравнения определяют вид переходных процессов. Поэтому можно определить ряд показателей качества по корням характеристического уравнения, не рассматривая переходные процессы.

Пусть дано характеристическое уравнение системы

,

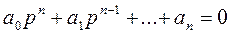с корнями р = р₁, р₂,…, р_n. При простых корнях характеристического уравнения собственная составляющая движения описывается уравнением

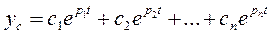. (1.10.3.1)

Каждое слагаемое в выражении (1) называется модой. Для асимптотической устойчивости всей системы необходимо и достаточно, чтобы каждая мода с течением времени стремилась к нулю, а для этого корни должны иметь отрицательные действительные части, т.е. на комплексной плоскости корни должны лежать слева от мнимой оси.

 

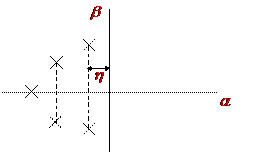
Рисунок 1.10.4. Заданная область расположения корней.

Моду для пары комплексно сопряженных корней 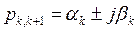можно представить в виде

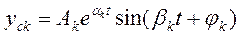. (1.10.3.2)

В случае одного действительного корня в (2) следует положить .

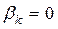Самое медленное затухание будет у мод, расположенных ближе всего к оси мнимых. Расстояние h от мнимой оси до ближайшего к ней корня называется степенью устойчивости. Степень устойчивости является показателем качества переходного процесса. Рассмотрим изменение амплитуды у самой медленно затухающей моды.

.

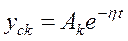Через промежуток времени, равный времени переходного процесса t_п, амплитуда станет равной , где введено в предыдущем пункте, то есть

,

откуда

. (1.10.3.3)

Таким образом, по степени устойчивости можно определить время переходного процесса t_п. Если d/у_уст=0,05, то при у_уст=1 d=0,05 и будем иметь

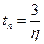. (1.10.3.4)

Из формул (3) и (4) следует, что размерность корней характеристического уравнения равна с^-1.

Как следует из (2), действительная часть характеризует затухание, а мнимая часть частоту колебаний. Для конкретной моды вводится понятие колебательности

.

Колебательностью всей системы является величина

.

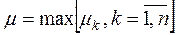Численное значение колебательности m не совпадает с колебательностью из предыдущего раздела, но характер поведения системы в зависимости от величины той или другой колебательности аналогичен. По корням характеристического уравнения можно определить затухание за период.

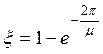. (1.10.3.5)

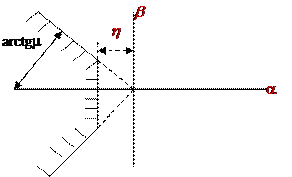
Для того чтобы система хорошо функционировала, её корни на плоскости корней должны занимать вполне определённое место, это место определяется степенью устойчивости (она должна быть не менее заданной) и колебательностью (она должна быть не больше заданной)

 

Рисунок 1.10.5.

Корни характеристического уравнения должны лежать в заштрихованной области. Из формулы (5)

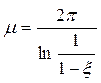, (1.10.3.6)

при x=0,98 m=p/2=1,57.

1.10.4 Интегральные показатели качества.Интегральные критерии дают общую оценку быстроты затухания и величины отклонения регулируемой переменной в совокупности.

При монотонных переходных процессах (рис. 1.10.6) может использоваться в роли интегрального критерия качества показатель качества

,

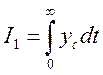где у_с – собственная составляющая движения. I₁ равен площади между кривой и осью абсцис.

 

Рисунок 1.10.6.

Чем меньше эта площадь, тем быстрее переходный процесс и тем меньше ошибка системы. Однако этот критерий не годится для знакопеременных переходных процессов.

 

 

Рисунок 1.10.7.

Для того чтобы этот критерий годился для знакопеременных переходных процессов, надо его модифицировать до вида

или .

Однако этот критерий не учитывает колебательности системы.

Чем выше колебательность системы, тем большие по модулю скорости возникают в переходных процессах. Поэтому, естественно, для того чтобы учесть (минимизировать) колебательность, в интегральный критерий качества должна быть включена скорость переходного процесса.

,

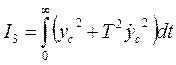где Т – весовой коэффициент, имеющий размерность времени. В процессе проектирования системы управления интегральный критерий качества должен минимизироваться. Рассмотрим предельный переходный процесс, который будет иметь место при минимизации критерия I₃.

.

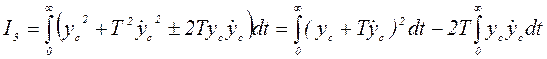т.к. система асимптотически устойчива, то у_с(µ)=0. Тогда

,

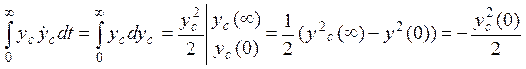где у(0) — начальное условие, которое обычно не оптимизируется т.к. зависит от случайных обстоятельств и является const. Окончательно получим

.

Минимизация осуществляется за счёт минимизации интеграла. Интеграл будет минимальным, когда подынтегральное выражение равно 0, т.е.

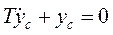(инерционное звено I порядка)

Решение данного уравнения показано на рис. 1.10.8.

 

Рисунок 1.10.8.

Из этого рисунка видно влияние весового коэффициента Т на вид предельного переходного процесса.