Главная | Обратная связь

Корневые критерии устойчивости

Как следует из рисунков 1.9.1-1.9.3, у_с не равен тождественно нулю, тогда из (5) следует

D(p)º0 . (1.9.1.1)

Уравнение (1) называется характеристическим уравнением, соответствующим уравнениям (1) и (5). Пусть это уравнение будет n-го порядка, тогда оно имеет n корней р₁, р₂,…, р_n. Если коэффициенты a₀, a₁,…,a_n — действительные, то корни уравнения (1) могут быть действительными и комплексными (комплексно-сопряженными).

.

Корни могут быть простыми (нет им равных) и кратными (равными). Кратность это количество равных корней. Если корни простые то решение уравнения (5) можно представить в виде

, (1.9.1.2)

где с₁, с₂,…, с_n — постоянные интегрирования, зависящие от начальных условий,

р₁, р₂,…, р_n — простые корни характеристического уравнения. В выражении (2) каждое слагаемое называется модой. Рассмотрим две моды, соответствующие паре комплексно-сопряженных корней.

. (1.9.1.3)

С помощью формулы Эйлера уравнение (3) можно представить в виде

, (1.9.1.4)

где А_к, j_к — новые постоянные интегрирования, зависящие от начальных условий.

На рис. 4 представлены различные виды переходных процессов моды (4) в зависимости от вида корней, соответствующих данной моде.

a_k>0, a_k<0, y_ck

 

 

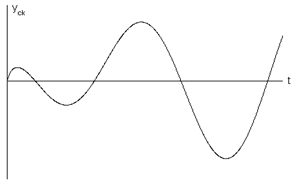
Рисунок 1.9.4

 

На основании рисунка 4 можно констатировать следующее.

Для того чтобы система была асимптотически устойчивой, необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения были отрицательными.

Для того чтобы система была неустойчивой, достаточно, чтобы хотя бы у одного корня действительная часть была положительной.

Для того чтобы система была гранично устойчивой, необходимо и достаточно, чтобы у части корней действительные части были равны нулю, причём среди этих корней не должно быть кратных, а у остальных корней действительные части должны быть меньше нуля.

В случае наличия кратных корней (например, p₁= p₂= p₃= p_1-3) вместо выражения (2) будет выражение (5).

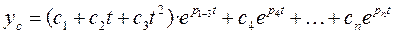. (1.9.5)

Выражение (5) позволяет заключить, что при мнимом корне p_1-3 нулевое решение будет неустойчивым за счет выражения в скобках.

Сформулируем приведенные критерии в геометрическом виде. На рис. 5 изображена плоскость корней, где крестиками обозначено расположение корней. С помощью этого рисунка приведенные критерии можно продемонстрировать следующим образом:

 

 

Рисунок 1.9.5 Расположение корней.

Для того чтобы система была асимптотически устойчивой необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости.

Для того чтобы система была неустойчивой, достаточно, чтобы хотя бы один корень находился в правой полуплоскости.

Для того чтобы система была гранично устойчивой, необходимо и достаточно, чтобы часть корней находилась на мнимой оси, причём, среди этих корней не должно быть совпадающих, а остальные корни должны лежать в левой полуплоскости.