Почленное дифференцирование и интегрирование степенных рядов.

Теорема:

Если степенной ряд

(1)

имеет радиус сходимости , то:

1) его можно почленно дифференцировать раз в интервале , причем ;

2) его можно почленно интегрировать раз в интервале , причем 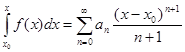, где .

3) Степенные ряды, полученные дифференцированием или интегрированием степенного ряда (1) имеют тот же радиус сходимости , что и исходный ряд.

Доказательство:

Первые два утверждения 1) и 2) очевидны, так как ряд (1) сходится равномерно в области . Третье утверждение следует, если к дифференцированному или интегрированному ряду применить признак Даламбера или Коши, например, для ряда (1)

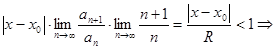
Для нахождения суммы степенного ряда часто удобно исследовать его дифференцирование или интегрирование.

7. Определить область сходимости функционального ряда.

а)

б)

в)

8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;

б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.

а)

б)

9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).

а)

10. а)Найти неопределённый интеграл;

б) Найти или вычислить, определённый интеграл;

в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).

а)

б)

в)

11. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по синусам.

12. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по косинусам.

Вариант№10

1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.

а)

б)

2. Исследовать ряды на сходимость по определению сходимости.

а)

б)

3. Исследовать ряды на сходимость с помощью признака сравнения.

а)

б)

4. То же с помощью признака Даламбера.

а)

б)

5. То же с помощью интегрального (Коши-Маклорена) признака.

а)

б)

6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.

а)

б)

Пример 37.

Найти сумму ряда .

Интервал сходимости ряда сразу следует из признака Коши

Продифференцировав этот ряд почленно

получим ряд геометрической прогрессии со знаменателем :

Проинтегрируем полученное выражение

, .

Пример 38.

Последовательно дифференцируя этот ряд, получаем:

Пример 39

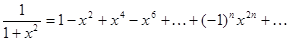, где .

Интегрируя этот ряд почленно (при ), получаем:

то есть

где .

Пример 40.

Интегрируя этот ряд почленно (при 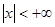) получаем:

, откуда

Функция называется бесконечно дифференцируемой в точке на интервале, если она имеет производные любого порядка в этой точке на этом интервале.

Ряд Тейлора

Пусть для является суммой степенного ряда по степеням разности , сходящегося в некотором интервале

Тогда в интервале сходимости, который симметричен относительно точки

, ряд можно дифференцировать любое число раз.

7. Определить область сходимости функционального ряда.

а)

б )

в)

8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;

б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.

а)

б)

9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).

а)

10. а)Найти неопределённый интеграл;

б) Найти или вычислить, определённый интеграл;

б)

б) ; в)

11. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по косинусам.

12. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по синусам.

Вариант№9

1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.

а)

б)

2. Исследовать ряды на сходимость по определению сходимости.

а)

б)

3. Исследовать ряды на сходимость с помощью признака сравнения.

а)

б)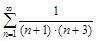

4. То же с помощью признака Даламбера.

а)

б)

5. То же с помощью интегрального (Коши-Маклорена) признака.

а)

б)

6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.

а)

б)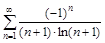

Дифференцируя, получаем:

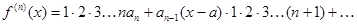
Пусть , тогда

то есть

Отсюда найдем

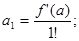
Подставим полученные выражения коэффициентов в ряд для ,

Рядом Тейлора функции по степеням или что то же, в окрестности точки называется степенной ряд вида:

(при этом предполагается, что бесконечно дифференцируема в точке )

При получим ряд по степеням 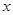, который называется рядом Маклорена функции .

Приведенными выше рассуждениями доказана теорема:

Если в некоторой окрестности точки является суммой степенного ряда по степеням , то этот ряд является рядом Тейлора функции .

Из этой теоремы как следствие получается теорема единственности:

Если функция в некоторой окрестности точки разложена в степенной ряд по степеням , то есть является суммой сходящегося в некоторой окрестности ряда по степеням , то такое разложение единственное.

Или иначе: не может быть двух различных степенных рядов по степеням , сходящихся к одной и той же функции. Это получается сразу, если учесть, что коэффициент ряда выражается через значения функции и ее производных в точке .

При практическом применении этой теоремы (для решения дифференциальных уравнений с помощью степенных рядов) используют следующую формулировку этой теоремы: если

имеются два тождественных сходящихся на некотором

7. Определить область сходимости функционального ряда.

а)

б)

в)

8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;

б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.

а)

б)

9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).

а)

10. а)Найти неопределённый интеграл;

б) Найти или вычислить, определённый интеграл;

а)

б) ; в)

11. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по синусам.

12. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по косинусам.

Вариант№8

1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.

а)

б)

2. Исследовать ряды на сходимость по определению сходимости.

а)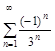

б)

3. Исследовать ряды на сходимость с помощью признака сравнения.

а)

б)

4. То же с помощью признака Даламбера.

а) 0

б)

5. То же с помощью интегрального (Коши-Маклорена) признака.

а)

б)

6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.

а)

б)

интервале ряда по степеням , то коэффициенты этих рядов при одинаковых степенях равны.

Таким образом, теорема единственности дает обоснование метода сравнения коэффициентов, который неоднократно использовался в курсе, в частности при разложении рациональных дробей на сумму элементарных дробей и при решении линейных дифференциальных уравнений методом подбора частных решений.

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒