Главная | Обратная связь

Рассмотрим три случая.

1. .

Из определения верхней грани следует, что при 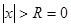ряд расходится и только при 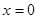он сходится. Следовательно в случае 1 область сходимости ряда сводится к точке 0 и характеризуется условием (2).

 

2. .

Пусть 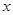- любое данное (фиксированное) число удовлетворяющее . Из определения следует, что существует такое значение 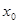из области сходимости ряда, что . По теореме Абеля из этого вытекает абсолютная сходимость ряда. Таким образом, в случае 2 область сходимости может быть охарактеризована одним из условий (1)-(4).

 

3. .

Пусть 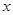- любое данное (фиксированное) число. По определению существует такое как угодно большое по абсолютной величине число 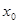(причем ), для которого ряд сходится. По теореме Абеля отсюда вытекает абсолютная сходимость ряда. Следовательно, в случае 3 ряд сходится для всех 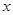, то есть областью его сходимости служит (-∞, +∞) (условие 1) и внутри ряд сходится абсолютно.

 

Радиус сходимости степенного ряда удобно находить с помощью признака Даламбера:

Если существует конечный или бесконечный предел ,

то .

В самом деле, если радиус определен по этой формуле, то по признаку Даламбера

.

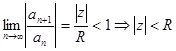Аналогично, легко получить выражение для радиуса с помощью формулы Коши:

Если существует конечный или бесконечный предел , то .

В этом случае формула имеет специальное название – Коши-Адамара.

Опять же, если радиус задается этой формулой, то

.

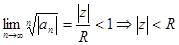Замечание:

После нахождения радиуса сходимости , следует исследовать граничные точки интервала сходимости. Для этого в исходный ряд подставим точки концов интервала, получим два числовых ряда. Исследование их на сходимость ответит на вопрос включать их в область сходимости или нет.

Пример 30.

Определить область сходимости ряда .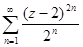

Применим признак Даламбера

 

7. Определить область сходимости функционального ряда.

а)

б)

в)

8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;

б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.

а)

б)

9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).

а)

10. а)Найти неопределённый интеграл;

б) Найти или вычислить, определённый интеграл;

в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).

а) ; б)

в)

11. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по косинусам.

12. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по синусам.

 

Вариант№13

1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.

а)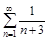

б)

2. Исследовать ряды на сходимость по определению сходимости.

а)

б)

3. Исследовать ряды на сходимость с помощью признака сравнения.

а)

б)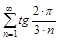

4. То же с помощью признака Даламбера.

а)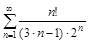

б)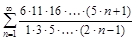

 

5. То же с помощью интегрального (Коши-Маклорена) признака.

а)

б)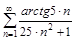

6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.

а)

б)

.

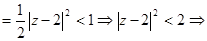
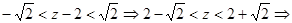
Исследуем граничные точки: , .

В первом случае имеем числовой ряд 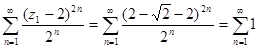- расходится.

Во втором случае имеем ряд , который также расходится.

 

Итак, область сходимости исследуемого ряда .

 

Пример 31.

Найти область сходимости ряда

Пусть при (при 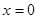ряд сходится).

Применим признак Даламбера:

;

отсюда видно, что заданный ряд

 

 

то есть

отсюда, в свою очередь, следует, что .

Следовательно, промежуток сходимости ряда есть .

Выясним вопрос о сходимости ряда на концах этого промежутка, то есть при и .

Подстановка этих значений в заданный ряд дает соответственно ряды:

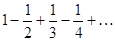
Первый из них сходится, второй расходится.

Таким образом, областью сходимости рассматриваемого ряда служит полу отрезок .

Пример 32.

Найти область сходимости ряда

Решение.

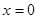Пусть при (при ряд сходится).

Применим признак Даламбера:

7. Определить область сходимости функционального ряда.

а)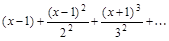

б)

в)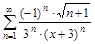

8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;

б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.

а)

б)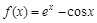

9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).

а)

10. а)Найти неопределённый интеграл;

б) Найти или вычислить, определённый интеграл;

в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).

а)

б)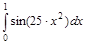

в)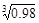

11. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по синусам.

12. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) по косинусам.

 

Вариант№12

1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.

а)

б)

2. Исследовать ряды на сходимость по определению сходимости.

а)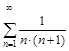

б)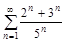

3. Исследовать ряды на сходимость с помощью признака сравнения.

а)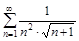

б)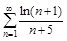

4. То же с помощью признака Даламбера.

а)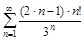

б)

5. То же с помощью интегрального (Коши-Маклорена) признака.

а)

б)

6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.

а)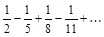

б)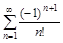

 

; отсюда видно, что заданный ряд

отсюда, в свою очередь, следует, сто .

Следовательно, промежуток сходимости ряда есть .

Выясним вопрос о сходимости ряда на концах этого промежутка, то есть при и .

Подстановка этих значений в заданный ряд дает соответственно ряды:

Оба они сходятся.

Таким образом, областью сходимости рассматриваемого ряда служит отрезок .

Пример 33.

Найти область сходимости ряда

Решение: Применяем признак Даламбера

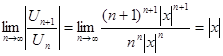
; отсюда очевидно, что заданный ряд расходится при любом значении ; это, в свою очередь, говорит о том, что . Следовательно, область сходимости заданного ряда сводится к точке 0.

 

Пример 34.

Найти область сходимости ряда

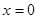Решение: Пусть при (при ряд сходится).

Применим признак Даламбера:

; отсюда видно, что заданный ряд сходится при любом значении 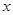; это, в свою очередь, говорит о том, что .

Следовательно, промежуток сходимости данного ряда есть , который служит и его область сходимости.

Пример 35.

Найти область сходимости ряда

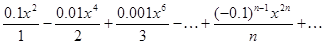
Решение.

Пусть при (при 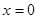ряд сходится).

Применим признак Даламбера:

;

отсюда видно, что заданный ряд

 

7. Определить область сходимости функционального ряда.

а)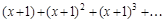

б)

в)

8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;

б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.

а)

б)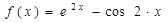

9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).

а)

10. а)Найти неопределённый интеграл;

б) Найти или вычислить, определённый интеграл;

в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).

а)

б) ; в)

11. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)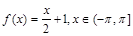

б) по синусам.

12. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) 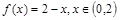по косинусам.

 

 

Вариант№11

1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.

а)

б)

2. Исследовать ряды на сходимость по определению сходимости.

а)

б)

3. Исследовать ряды на сходимость с помощью признака сравнения.

а)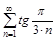

б)

4. То же с помощью признака Даламбера.

а)

б)

5. То же с помощью интегрального (Коши-Маклорена) признака.

а)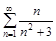

б)

6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.

а)

б)

 

то есть

отсюда, в свою очередь, следует, сто .

Рассуждая далее так же, как в примере 1, мы придем к заключению, что областью сходимости заданного ряда служит отрезок .

 

Пример 36.

Найти область сходимости ряда

Пусть при (при 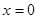ряд сходится).

Применим признак Даламбера:

.

Рассуждая далее так же, как в примере 4, мы придем к заключению, что областью сходимости заданного ряда служит промежуток .