 |
|
Основные разложения
Запишем ряд Макларена

1.Пусть  ,тогда
,тогда

при 
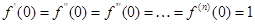 ,
,
следовательно
 ;
;
 ,
,
так как  ,
,  ,
, 
 на основании леммы:
на основании леммы:
Для любого 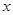 :
: 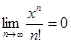 , т.е.
, т.е.

| | |||
| |
7. Определить область сходимости функционального ряда.
а) 
б) 
в) 
8. а) Разложить  в ряд Тейлора по степеням разности
в ряд Тейлора по степеням разности  ,пользуясь определением ряда Тейлора;
,пользуясь определением ряда Тейлора;
б) Разложить  в ряд Маклорена, пользуясь стандартными разложениями.
в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б) 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 

10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 
б)  ; в)
; в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)  по косинусам.
по косинусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)  по синусам.
по синусам.
Вариант№7
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 


3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 
б) 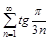
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б) 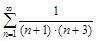
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б) 
2.Пусть  , тогда
, тогда
| |

Пусть х=0, тогда f(x)=0

 .
.
Отсюда следует:
 .
.
Это условие в силу леммы даёт  .
.
Следовательно, при любом x:
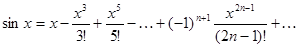
| |
Аналогично для 
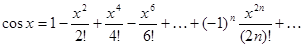
Пример 41.
Рассмотрим ряд  .
.
Он равномерно сходится на  , где
, где  и сумма его равна
и сумма его равна  , то есть
, то есть 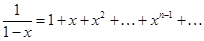
Проинтегрируем при 


или 

Заменим 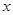 на
на 

 .
.
Пример 42.
Разложить в ряд Маклорена функцию 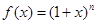 ,
,
где  - любое действительное число
- любое действительное число 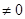 .
.
Составим ряд Маклорена для данной функции.
Имеем:


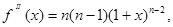

| | |||
| | |||
7. Определить область сходимости функционального ряда.
а) 
б) 
в) 
8. а) Разложить  в ряд Тейлора по степеням разности
в ряд Тейлора по степеням разности  ,пользуясь определением ряда Тейлора;
,пользуясь определением ряда Тейлора;
б) Разложить  в ряд Маклорена, пользуясь стандартными разложениями.
в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б) 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 

10. б)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 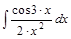
б)  ; в)
; в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)  по синусам.
по синусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 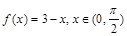 по косинусам
по косинусам
Вариант№6
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 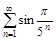
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 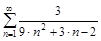


3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 
б) 
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б) 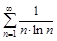
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б) 


Следовательно,


Ряд в правой части формулы называется биномиальным рядом.
Для определения интервала сходимости воспользуемся признаком Даламбера:
Пусть  , тогда
, тогда
 .
.
Следовательно, ряд сходится при  и расходится при
и расходится при
 .
.
Следовательно, интервал сходимости данного ряда  .
.
| | |||
| |
Пример 43.
Разложить в ряд функцию
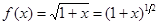
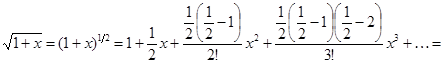


Пример 44.
Разложить в биномиальный ряд функцию

 (при условии
(при условии  )
)
Пример 45.
Разложить в ряд Маклорена функцию

Заметим, что 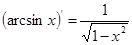 .
.
Проинтегрируем выражение
 в пределах от 0 до х, получаем
в пределах от 0 до х, получаем
 .
.