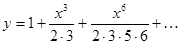 |
|
Решение дифференциального уравнения
Рассмотрим линейное дифференциальное уравнение n-го порядка.
(1)
коэффициент при 
равен 1.
Теорема:
| |
| |
, то сходящиеся в некоторой окрестности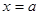 
, то решение этого уравнения удовлетворяющее начальным условиям: 
, 
, 
, 
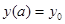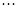разлагается в степенной ряд по степеням 
, сходящийся по крайней мере в меньшем из интервалов сходимости рядов для коэффициентов и правой части дифференциального уравнения.
Практически решение дифференциального уравнения в виде степенного ряда можно получить двумя способами:
1. сравнение коэффициентов;
2. последовательное дифференцирование.
1. Способ сравнения коэффициентов заключается в следующем: сначала записывают решение в виде степенного ряда с неотрицательными коэффициентами
Затем из начальных условий определяют значения коэффициентов 
, 
, , 
. После этого подставляют в дифференциальное уравнение вместо 
и производных соответствующие степенные ряды, а также вместо коэффициентов и правой части записывают их разложения в степенные ряды по степеням 
и производят действия над рядами. Затем сравнивают коэффициенты при одинаковых степенях . Из полученных таким путем уравнений определяют коэффициенты ряда.
Пример 48.
начальные условия 
, 
Решение ищем в виде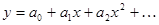 
Из начальных условий: 
, 
.
Затем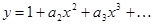 
подставляем в исходное
уравнение.
| | |||
| |
7. Определить область сходимости функционального ряда.
а) 
б) 
в) 
8. а) Разложить 
в ряд Тейлора по степеням разности 
,пользуясь определением ряда Тейлора;
б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б)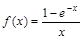 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а)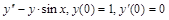 
10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а)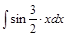 
б) 
; в)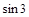 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по синусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по косинусам.
Вариант№4
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а)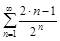 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 
3. Исследовать ряды на сходимость с помощью признака сравнения.
а)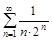 
б) 
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б) 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а)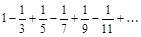 
б) 
Сравниваем коэффициенты:
таким образом 