 |
|
Свойства равномерно сходящихся рядов
Теорема 1
Равномерно сходящийся ряд 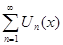 на
на  непрерывных функции
непрерывных функции  имеет в качестве своей суммы непрерывную функцию
имеет в качестве своей суммы непрерывную функцию  .
.
Теорема 2
| |
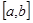 ряд
ряд 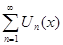 с непрерывными членами можно интегрировать почленно на этом отрезке, то есть ряд составленный из интегралов от его членов на отрезке
с непрерывными членами можно интегрировать почленно на этом отрезке, то есть ряд составленный из интегралов от его членов на отрезке 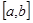 сходится к интегралу от суммы ряда по этому отрезку.
сходится к интегралу от суммы ряда по этому отрезку.
| |
Теорема 3
Если члены ряда
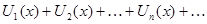
непрерывно дифференцируемые функции на  и ряд сходится к функции
и ряд сходится к функции  на
на  , а ряд
, а ряд

равномерно сходится на этом отрезке, то его сумма равна 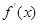 , то есть
, то есть
 или (2)
или (2)
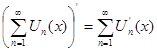 . (3)
. (3)
Если ряд 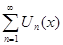 на
на  удовлетворяет (3), то говорят, что этот ряд можно почленно дифференцировать.
удовлетворяет (3), то говорят, что этот ряд можно почленно дифференцировать.
Действительно, из условия теоремы получаем  на
на  и
и 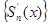 равномерно сходится на этом отрезке, так как
равномерно сходится на этом отрезке, так как

по теореме для последовательности 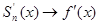 на
на  , то получим
, то получим 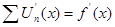 .
.
Замечание.
Если последовательность дифференцируемых функции 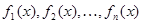
равномерно сходится к  на
на  ,то последовательность производных этих функций:
,то последовательность производных этих функций:
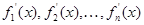 ,
,
| |
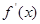 на этом отрезке.
на этом отрезке.
| |
7. Определить область сходимости функционального ряда.
а) 
б) 
в) 
8. а) Разложить  в ряд Тейлора по степеням разности
в ряд Тейлора по степеням разности  ,пользуясь определением ряда Тейлора;
,пользуясь определением ряда Тейлора;
б) Разложить  в ряд Маклорена, пользуясь стандартными разложениями.
в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б) 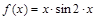
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 

10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 
б) 
в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)  по синусам.
по синусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)  по косинусам.
по косинусам.
Вариант№16
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 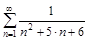

3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 
б) 
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б) 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б) 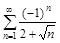
Это подтверждается примером последовательности функций 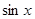 ,
, 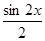 ,
, 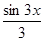 , …,
, …,  , …, которые сходятся к
, …, которые сходятся к  равномерно на любом отрезке
равномерно на любом отрезке  между тем, как последовательность производных этих функций
между тем, как последовательность производных этих функций 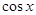 ,
,  , …,
, …,  , … расходится в точке
, … расходится в точке 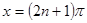
Пример 27.
Ряд 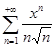 сходится равномерно в отрезке
сходится равномерно в отрезке 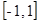 .
.
Поэтому из 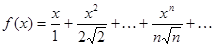 получаем:
получаем:
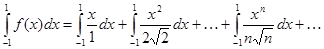 ,
,
то есть
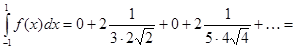
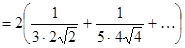 .
.
Пример 28.
Ряд 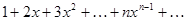 сходится равномерно в отрезке
сходится равномерно в отрезке  , где
, где  , при любом значении
, при любом значении 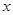 из этого отрезка имеем:
из этого отрезка имеем:
 ,
,
а знакоположительный числовой ряд 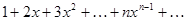
сходится (по признаку Даламбера).

| |
 :
:
| |

то есть
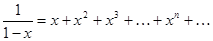 ,
,
равномерно сходящийся в отрезке  .
.
Пример 29.
Ряд 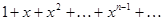 равномерно сходится в отрезке
равномерно сходится в отрезке  , где
, где  , для любого значения
, для любого значения 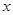 из этого отрезка имеем:
из этого отрезка имеем: 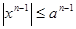 , а знакоположительный числовой ряд
, а знакоположительный числовой ряд 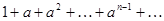 , являясь бесконечно убывающей геометрической прогрессией, сходится.
, являясь бесконечно убывающей геометрической прогрессией, сходится.
Поэтому из

получаем 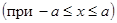 :
:

то есть

Степенные ряды
Степенным рядом называется ряд вида:
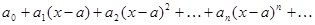 (1)
(1)
или 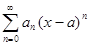
| |
| |
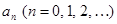 - числа, называемые коэффициентами ряда.
- числа, называемые коэффициентами ряда.
7. Определить область сходимости функционального ряда.
а) 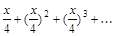
б) 
в) 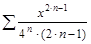
8. а) Разложить  в ряд Тейлора по степеням разности
в ряд Тейлора по степеням разности  ,пользуясь определением ряда Тейлора;
,пользуясь определением ряда Тейлора;
б) Разложить  в ряд Маклорена, пользуясь стандартными разложениями.
в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б) 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 

10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 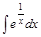
б)  ; в)
; в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)  по синусам.
по синусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 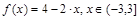
б) 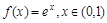 по косинусам.
по косинусам.
Вариант№15
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 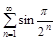
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 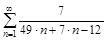


3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 
б) 
4. То же с помощью признака Даламбера.
а) 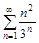
б) 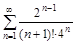
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 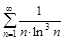
б) 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 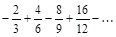
б) 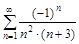
Степенной ряд (1) называется также рядом по степеням разности  .
.
Если  , то получим
, то получим  (2) или ряд по степеням
(2) или ряд по степеням 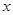 . Ряд (1) сводится к (2) с помощью подстановки
. Ряд (1) сводится к (2) с помощью подстановки 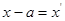 .
.
Теорема Абеля
Если степенной ряд  сходится для значений
сходится для значений 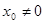 , то он абсолютно сходится для всех значений
, то он абсолютно сходится для всех значений 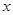 удовлетворяющих неравенству
удовлетворяющих неравенству  .
.
Доказательство: Числовой ряд 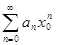 является сходящимся (по условию) Поэтому его общий член Un=
является сходящимся (по условию) Поэтому его общий член Un= 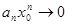 и, следовательно, представляет собой ограниченную величину, то есть существует такое число
и, следовательно, представляет собой ограниченную величину, то есть существует такое число 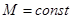 , что для всех
, что для всех

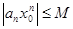
Если  то
то  ,
,
Тогда:
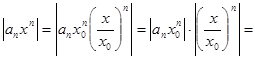
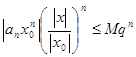 ,
,
то есть
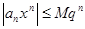 .
.
| |
| |
 - общий член убывающей геометрической прогрессии:
- общий член убывающей геометрической прогрессии:  , которая сходится, и тогда по признаку сравнения
, которая сходится, и тогда по признаку сравнения 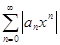 сходится и, следовательно,
сходится и, следовательно,  сходится абсолютно при
сходится абсолютно при  .
.
Следствие:
Если степенной ряд (1) расходится при 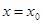 , то он расходится и при всяком
, то он расходится и при всяком 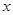 больше по абсолютной величине, чем
больше по абсолютной величине, чем 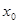 , то есть при
, то есть при 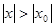 .
.