 |
|
Вычисление неопределенного и определенного интегралов
Пример 50.
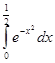
Разложим подинтегральную функцию в ряд:
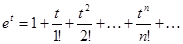
подставим вместо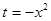 
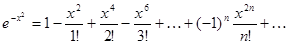
Почленно интегрируя, получаем:
| |
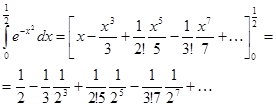
Знакочередующийся ряд удовлетворяет условиям Лейбница. Следовательно, ошибка при замене суммы ряда его частичной суммой по абсолютной величине меньше, чем абсолютная величина первого из отброшенных его членов. Возьмем первых два слагаемых
| |
7. Определить область сходимости функционального ряда.
а)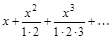 
б)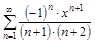 
;
в)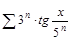 
8. а) Разложить 
в ряд Тейлора по степеням разности 
,пользуясь определением ряда Тейлора;
б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б)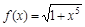 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а)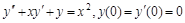 
10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а)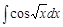 
б)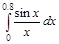 
; в)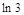 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а)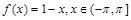 
б)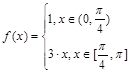 
по синусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а)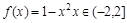 
б)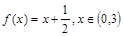 
по косинусам.
Вариант№3
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а)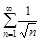 
б)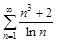 
2. Исследовать ряды на сходимость по определению сходимости.
а)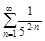 
б)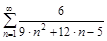 
3. Исследовать ряды на сходимость с помощью признака сравнения.
а)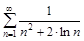 
б)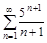 
4. То же с помощью признака Даламбера.
а)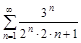 
б)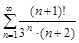 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а)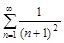 
б) 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б)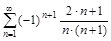 
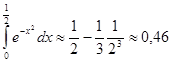
Пример 51.
Вычислить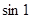 
с пятью знаками.
Положим 
. В стандартном разложении
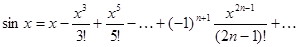
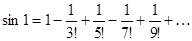
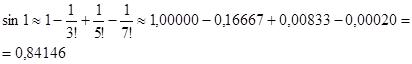Пример 52..
Вычислить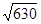 
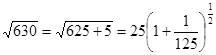
Берем биномиальный ряд:
| | |||
| |
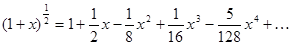
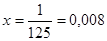
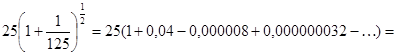
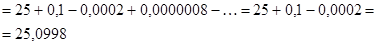
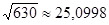
Ряды Фурье