Главная | Обратная связь

Ряд Фурье для функций периода 2p

 

Равномерная сходимость на отрезке 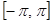данного тригонометрического ряда не нарушится, если ряд умножить на или .

По условию

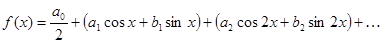
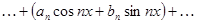(2)

при этом ряд равномерно сходится на отрезке 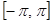, так как непрерывна, то существует.

В результате почленного интегрирования равномерно сходящегося ряда (2) получаем: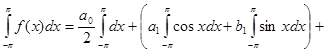

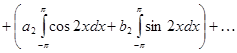
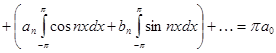
откуда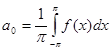

Умножая (2) на и интегрируя его в пределах от 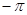до 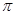, получим:

7. Определить область сходимости функционального ряда.

а)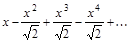

б) 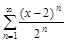; в)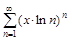

8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;

б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.

а)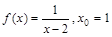

б)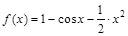

9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).

а)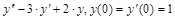

10. а) Найти неопределённый интеграл;

б) Найти или вычислить, определённый интеграл;

в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).

а) 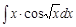; б) ; в)

11. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)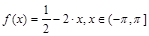

б) 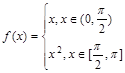по синусам.

12. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)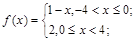

б) 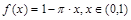по косинусам.

 

 

Вариант№1

1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.

a)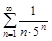

б)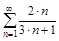

2. Исследовать ряды на сходимость по определению сходимости.

а)

б)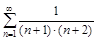

3. Исследовать ряды на сходимость с помощью признака сравнения.

а)

б)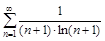

4. То же с помощью признака Даламбера.

а)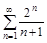

б)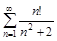

5. То же с помощью интегрального (Коши-Маклорена) признака.

а)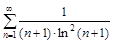

б)

6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.

а)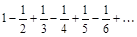

б)

 

 

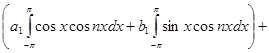
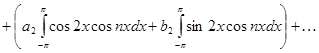
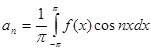
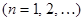
Умножая (2) на и интегрируя его получим:

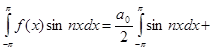
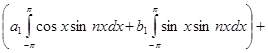
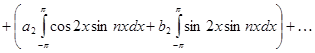
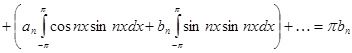
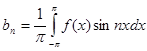
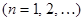
Таким образом, получены следующие выражения для коэффициентов ряда:

 

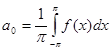
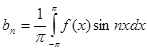
Или объединяя первые два равенства запишем:

(3)

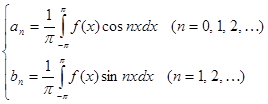
в (3) пределы интегрирования можно взять от до (на основании свойства периодичности функций) или от до , где - любое число.

Пусть - любая периодическая функция периода , на промежутке и имеющая на этом промежутке конечное число точек разрыва первого рода.

Тогда для функции коэффициенты определяемые (3) существуют и называются коэффициентами Фурье этой функции.

Рядом Фурье некоторой функции называется тригонометрический ряд коэффициенты которого определяются по формулам (3).

Таким образом:

Если является суммой равномерно сходящегося на отрезке тригонометрического ряда, то этот ряд является рядом Фурье функции .

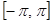Не существует двух тригонометрических рядов равномерно сходящихся на отрезке к одной и той же функции, или что то же, если функция разложена в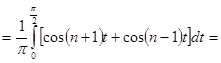

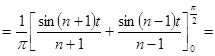
или (после соответствующих преобразований)

;

;

.

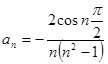
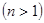Таким образом, для отрезка имеем:

.

 

 

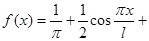
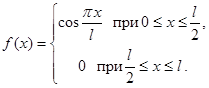
Образуем новую функцию путем четного продолжения данной функции с отрезка на отрезок 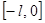и последующего периодического продолжения за пределами отрезка 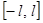. Функция удовлетворяет, очевидно, условиям разложимости в ряд Фурье.

На отрезке имеем:

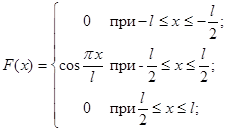
здесь функция является четной, так как соответствующий график симметричен оси Оу.

Поэтому имеем:

;

 

 

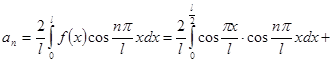
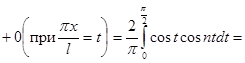
равномерно сходящийся тригонометрический ряд на отрезке 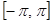, то такое разложение единственное.