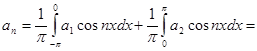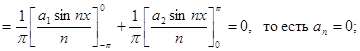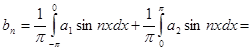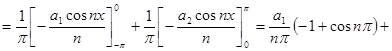|
|
Теорема 1. (Теорема Дирихле).
Если функция  имеет место период
имеет место период  и на отрезке
и на отрезке 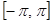 непрерывна или имеет конечное число точек разрыва первого рода, и
непрерывна или имеет конечное число точек разрыва первого рода, и 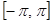 можно разбить на конечное число отрезков так, что внутри каждого из них функция
можно разбить на конечное число отрезков так, что внутри каждого из них функция  монотонна, то ряд Фурье функции
монотонна, то ряд Фурье функции  сходится при любом
сходится при любом 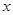 , причем в точках непрерывности функции
, причем в точках непрерывности функции  его сумма равна
его сумма равна  , а в точках разрыва
, а в точках разрыва  его сумма равна
его сумма равна 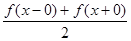 , то есть среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функции
, то есть среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функции  сходится равномерно на любом отрезке, который вместе со своими концами принадлежит интервалу непрерывности функции
сходится равномерно на любом отрезке, который вместе со своими концами принадлежит интервалу непрерывности функции  .
.
Замечание:
Функция, удовлетворяющая условиям теоремы Дирихле, называется кусочно-монотонной.
Теорема 2.
Если функция  имеет период
имеет период  , кроме того, функция
, кроме того, функция  и ее производная
и ее производная 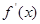 - непрерывные функции на отрезке
- непрерывные функции на отрезке 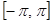 или имеют конечное число точек разрыва первого рода на этом отрезке, то ряд Фурье функции
или имеют конечное число точек разрыва первого рода на этом отрезке, то ряд Фурье функции  сходится при всех значениях
сходится при всех значениях 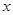 , причем в точках непрерывности функции
, причем в точках непрерывности функции  его сумма равна
его сумма равна  , а в точках разрыва функции
, а в точках разрыва функции  сумма равна
сумма равна 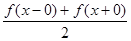 . При этом ряд Фурье функции
. При этом ряд Фурье функции  сходится равномерно на любом отрезке, который вместе со
сходится равномерно на любом отрезке, который вместе со
| | |||
| | |||
своими концами принадлежит интервалу непрерывности функции  .
.
Замечание:
Функция  , удовлетворяющая условиям этой теоремы кроме быть может условия периодичности, называется кусочно-гладкой на отрезке
, удовлетворяющая условиям этой теоремы кроме быть может условия периодичности, называется кусочно-гладкой на отрезке 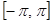 .
.
 |
Пример 53.
Разложить в ряд Фурье периодическую функцию  с периодом
с периодом 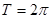 , заданную в
, заданную в  уравнением
уравнением  .
.
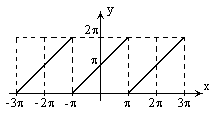 |
Графиком этой функции в
 является отрезок, соединяющий точки
является отрезок, соединяющий точки 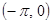 и
и  .
.
| |
| |

Полученный ряд Фурье сходится в точках разрыва  ,
,  ,
, 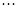 к
к  .
.
Пример 62.
Разложить периодическую функцию  :
:
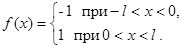
в ряд Фурье.
Решение
Данная функция удовлетворяет условиям разложимости в ряд Фурье; в промежутке  она является нечетной, так как здесь ее график симметричен относительно начала координат.
она является нечетной, так как здесь ее график симметричен относительно начала координат.
Поэтому имеем:
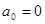 ;
;
 ;
;


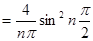 ,
,
то есть
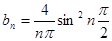 .
.
Таким образом,
 .
.
Пример 61.
Разложить в ряд по косинусам функцию:
 ;
;


 ,
,
то есть
 ;
;

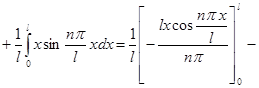
 ,
,
то есть
 .
.
Таким образом,

 .
.
 (так как подинтегральная функция второго интеграла – нечетная)
(так как подинтегральная функция второго интеграла – нечетная)

Следовательно, разложение функции  в ряд Фурье имеет вид:
в ряд Фурье имеет вид:
 .
.
Пример 54.
Разложить периодическую функцию  :
:

в ряд Фурье.
Решение
Данная функция удовлетворяет условиям теоремы 2. Имеем:
| | |||
| | |||
 |

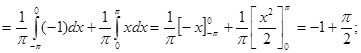
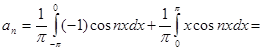

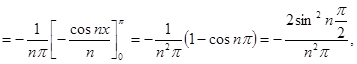
то есть
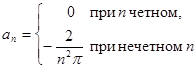
| |
 мы применили метод интегрирования по частям);
мы применили метод интегрирования по частям);
| |
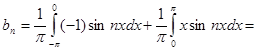
 (4”)
(4”)
и ряд (3) принимает вид:

Ряд

| |
Пример 61.
Разложить периодическую функцию  :
:

в ряд Фурье.
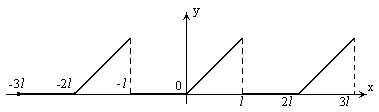 |
Данная функция удовлетворяет условиям разложимости в ряд Фурье.
Имеем:
 (4)
(4)
Если  – функция периода
– функция периода  , кусочно-гладкая или кусочно-монотонная на отрезке
, кусочно-гладкая или кусочно-монотонная на отрезке  , то она разлагается в ряд Фурье, то есть (3) справедливо.
, то она разлагается в ряд Фурье, то есть (3) справедливо.
В точках разрыва функции  сумма ряда Фурье равна
сумма ряда Фурье равна 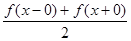 .
.
Замечание:
Для четной функции  :
:
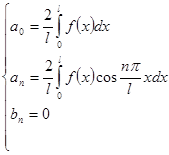 (4’)
(4’)
и ряд (3) принимает вид:
 .
.
Для нечетной функции  :
:
| |
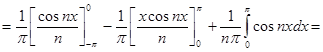

то есть
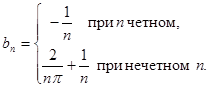
Таким образом, искомое разложение будет:
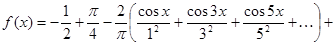
 .
.
Пример 55.
Разложить периодическую функцию  :
:

в ряд Фурье.
Решение
 |
Данная функция удовлетворяет условиям теоремы 2. Имеем:

| |