 |
|
Ряды Фурье для четных и нечетных функций с периодом 2p
Воспользуемся тем свойством, что интеграл по симметричному промежутку:
| |
 (1)
(1)
Заметим, что произведение двух четных или двух нечетных функций есть функция четная, а произведение четной функции на нечетную – нечетная функция.
Пусть f(x) – четная периодическая функция с периодом  , удовлетворяющая условиям разложимости в ряд Фурье, тогда используя свойство интеграла (1), получим:
, удовлетворяющая условиям разложимости в ряд Фурье, тогда используя свойство интеграла (1), получим:
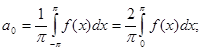

 ;
;
| |
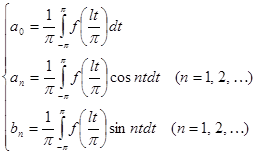 (2)
(2)
так как  , то
, то  ,
, 
| x | -p | p |
| t | -l | l |
Получаем:
 (3)
(3)
при этом

Рядом Фурье любой функции  периода
периода  непрерывной или имеющей конечное число точек разрыва первого рода на
непрерывной или имеющей конечное число точек разрыва первого рода на 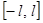 называется тригонометрический ряд вида:
называется тригонометрический ряд вида:
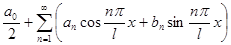 ,
,
где коэффициенты равны:
 ;
;  .
.
Таким образом, для отрезка  имеем:
имеем:
 .
.
Ряды Фурье для функций любого периода
Пусть  - периодическая функция периода
- периодическая функция периода 
(  - полупериод) кусочно-гладкая или кусочно-монотонная на отрезке
- полупериод) кусочно-гладкая или кусочно-монотонная на отрезке 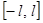 . Полагая
. Полагая  , получим функцию
, получим функцию  аргумента
аргумента  , период которой равен
, период которой равен  .
.
Подберем а так, чтобы период  был равен
был равен  , то есть,
, то есть,
 ,
,  .
.
Тогда подстановка  (сжатие или растяжение по оси Ох) приводит к функции
(сжатие или растяжение по оси Ох) приводит к функции  периода
периода  .
.
Эта функция удовлетворяет условиям разложимости в ряд Фурье, так как она кусочно-гладкая или кусочно-монотонная на отрезке 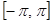 .
.
Разлагая функцию  в ряд Фурье, получим:
в ряд Фурье, получим:
 (1)
(1)
где

 ,
,
таким образом ряд Фурье для четной функции содержит только четные функции – косинусы и записывается так:
 (2)
(2)
при этом


Если f(x) – нечетная периодическая  функция, удовлетворяющая условиям разложимости в ряд Фурье, то
функция, удовлетворяющая условиям разложимости в ряд Фурье, то
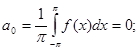

 ;
;

 .
.
Следовательно, ряд Фурье для нечетной функции содержит только нечетные функции – синусы:
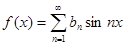 ,
,
где 
 .
.
Замечание 1:
Если функция  задана на
задана на  (или
(или  ) и удовлетворяет условиям разложимости в ряд Фурье, то в этом отрезке, или интервале ее можно бесчисленным множеством способов разложить в ряд Фурье.
) и удовлетворяет условиям разложимости в ряд Фурье, то в этом отрезке, или интервале ее можно бесчисленным множеством способов разложить в ряд Фурье.
| | |||
| |
Замечание2
Функцию  можно разложить в ряд по косинусам или синусам, для этого нужно продолжить функцию
можно разложить в ряд по косинусам или синусам, для этого нужно продолжить функцию  с заданного промежутка соответственно на промежуток
с заданного промежутка соответственно на промежуток  (или
(или 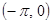 ) соответственно четным или нечетным образом, исходя из условия:
) соответственно четным или нечетным образом, исходя из условия:

 Пример 56.
Пример 56.
Разложить в ряд Фурье функцию
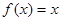 , при
, при 
 |
Функция
 является четной, так как
является четной, так как  , поэтому имеем:
, поэтому имеем:


| |
Данная периодическая функция  является непрерывной на всей оси Ох.
является непрерывной на всей оси Ох.
Пример 60.
Разложить в ряд по косинусам функцию 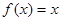 , заданную на отрезке
, заданную на отрезке  .
.
Решение.
 |
Образуем новую функцию
 путем четного продолжения данной функции
путем четного продолжения данной функции  с отрезка
с отрезка  на отрезок
на отрезок 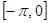 и последующего периодического продолжения
и последующего периодического продолжения  за пределами отрезка
за пределами отрезка 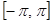 . Функция
. Функция  удовлетворяет, очевидно, условиям теоремы .
удовлетворяет, очевидно, условиям теоремы .
На отрезке 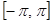 имеем:
имеем:

здесь функция  является четной, так как соответствующий график симметричен оси Оy.
является четной, так как соответствующий график симметричен оси Оy.
Поэтому имеем:


 ,
,
| |
 Пример59
Пример59
Разложить в ряд Фурье периодическую функцию заданную на отрезке 
f(x)=  .
.
Данная функция удовлетворяет условиям теоремы 2. На отрезке  функция четная, так как f(-x)=f(x) поэтому имеем:
функция четная, так как f(-x)=f(x) поэтому имеем:



 |

и тогда разложение данной функции в ряд Фурье будет иметь следующий вид: 
 ,
,
то есть
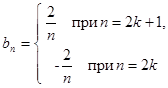
То для  имеем:
имеем:
 .
.
Согласно т. Дирихле полученный ряд Фурье сходится в точках разрыва  ,
,  ,
,  ,
, 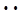 к нулю.
к нулю.
Пример 57.
Данная периодическая функция является непрерывной на всей оси Ох.
Разложить в ряд Фурье функцию  периода
периода  , изображенную на рисунке.
, изображенную на рисунке.
 |
Решение.
| |
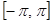 она является нечетной, так как здесь
она является нечетной, так как здесь
| |
график симметричен относительно начала координат. На отрезке  имеем:
имеем:

Поэтому имеем: 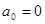 ;
;  ;
;
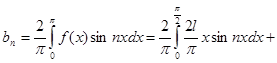
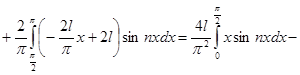
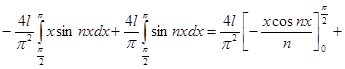

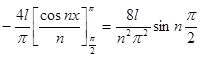 ,
,
то есть 
(при нахождении  мы применили метод интегрирования по частям).
мы применили метод интегрирования по частям).
Таким образом,
 .
.
| |
Данная периодическая функция  является непрерывной на всей оси Ох.
является непрерывной на всей оси Ох.
Пример 58.
Разложить в ряд Фурье периодическую функцию
f(x)=x2,
заданную на отрезке  .
.
Данная функция удовлетворяет условиям теоремы 2. На отрезке  функция четная, так как f(-x)=f(x) поэтому имеем:
функция четная, так как f(-x)=f(x) поэтому имеем:




при нахождении ап дважды была использована формула интегрирования по частям
Так как функция четна то при разложении в ряд Фурье коэффициент bn = 0
| |
 будет иметь вид:
будет иметь вид: