Главная | Обратная связь

Сложение натуральных чисел

Определение. Сложением натуральных чисел назы­вается такое соответствие, которое каждымнатуральным числам а и b сопоставляет одно и только одно натуральное число а + b и обладает следующими свойствами:

1) а+ 1 = а' для любого а N,

2) а+ b' =(а + b)' для любых a иb N.

Числа а и b называются слагаемыми, ачисло а + b — их суммой.

Встает вопрос о существовании и единственности операции сложения натуральных чисел. Прежде чем ответить на этот вопрос, проверим вначале существование некоторых функций на множестве N.

Теорема 1.Для любого элемента а из множества натуральных чисел, существует функция f_a(x):N→N, обладающее следующими свойствами:

1.f_a(1)=a', (1)

2.f_a(b')=[f_a(b)]'. (2)

Отметим, что для каждого элемента а подбирается своя функция, обозначаемая знаком f_a, который является слитным символом, не имеющим каких-либо частей.

Доказательство. Рассмотрим подмножество М во множестве N, где

М = {а N | функция f_a существует}.

Достаточно проверить, что М = N. Установим это равенство с помощью аксиомы индукции. Докажем истинность се посылок 1) и 2).

1) Проверим, что 1 М, т.е. существует функция f₁ обладающая следующими свойствами:

f₁ (l) = l', (3)

f₁ (b') = [f₁ (b)]'. (4)

Определим функцию f₁ по правилу

f₁ (x)= х'. (5)

Тогда f₁ (l) = 1', что и нужно в (3).

Проверим выполнение второго равенства (4) для функции f₁ . По правилу задания функции f₁ в (5) имеем f₁ (b') = (b')' и [f₁ (b)]' = (b')' Получили выполнение второго свойства для функции f₁. Итак, 1 М.

2) Проверим, что а М влечет а' М. Дано а М. Поэтому существует функция f_a,(х) с условиями (1) и (2). Требуется доказать, что а' М, т.е. нужно найти функцию f_а'(х), также удовлетворяющую данным условиям.

Зададим искомую новую функцию f_а'(х) через имеющуюся старую функцию f_a(x) по правилу

f_а'(х) = [f_a(x)]' (6)

Проверим выполнение условий (1) и (2) для новой функции f_а'(х). Для записи этих условий нужно заменить букву а на а'. Поэтому, проверяемые условия имеют вид

1. f_а'(1) = (a')' (7)

2. f_а'(b') = [f_a' (b)]' (8)

Установим выполнение первого условия. Применим определение (6) функции f_а'(х)при х = 1 и получим f_а'(1) = [f_а(1)]'. Так как старая функция f_а удовлетворяет условию (1), то f_а (1) = а'. Поэтому, [f_а (1)]' = (а')', что и нужно.

Проверим выполнимость второго (8). Рассмотрим левую часть f_а'(b'). По определению функции f_а'(х) и второму условию для f_а имеем f_а'(b') = [f_а(b')]' = [(f_а(b))']'. Правая часть [f_a' (b)]' равна [(f_а(b))']' по определению функции f_а'(х) и совпадает с левой частью. Итак, а' М и пункт 2) доказан. Ч. т. д.

Теорема 2.Операция сложения существует.

Доказательство. Определим операцию + на множестве N, используя функцию f_a(x) из предыдущей теоремы. Пусть а, b N. Считаем, что

a+b=f_а(b) (9)

Проверим первое условие из определения операции сложения, т.е. a + 1 = а'. По определению (9) имеем a + 1 = f_a(1). По (1) верно f_a(1) = а'. Получили a + 1 = а'.

Второе условие из определения операции сложения имеет вид а + b' = (а + b)'. По определению сложения а + b' = f_а(b'). По (2) верно равенство f_a(b')=[f_a(b)]'. Поэтому а + b' =[f_a(b)]'. Правая часть (а+b)' имеет вид [f_a(b)]' и равна левой части. Итак, для операции + выполняются два требуемых условия. Ч. т. д.

 

Теорема 3.Операция сложения, определена однозначно.

Доказательство. Требуется проверить, что не существует двух различных операций сложения + и. Для этого допустим, что обе операции + и 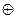явля­ются операциями сложения. Нужно установить, что a, b N a+b= a 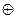b, т.е. операции + и 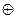совпадают.

Зафиксируем произвольный элемент а N и рассмотрим множество

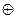М = {b N : а+b = а b}.

Достаточно проверить, что М = N.

1) Установим, что 1 М, т.е. а + 1 = a 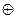1. Так как операция + является операцией сложения, то a + 1 = а'. Аналогично, операция 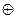является сложе­нием и, поэтому, a 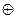1 = а'. Из a + 1 = а' и a 1 = а' получаем а + 1 = а 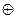1, что и нужно.

2) Пусть b М, т.е. a+b= a 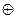b. Покажем, что b' М, т.е. a+b'= a 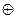b'. Так как + и 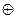— операции сложения, то a + b'= (а+b)' и a 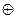b'= (а 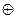b)'. Применяя a+b= a 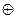b, получим a + b' = a 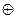b', т.е. b' М. Отсюда М =N. Ч. т. д.

Законы сложения

 

Теорема 1.Операция сложения на множестве натуральных чисел ассоциативна, т.е.

х, у, z N (х + у) + z = х + (у + z).

Доказательство. Доказательство проведем индукцией по z при произвольно выбранных x и y. При z=1 получаем

(х + у) + 1 = /опр. сложения п.1)/= (х + у)'=/опр. сложения п.2)/= х + у'= =/опр. сложения п.1)/= х + (у + 1).

Предположим, что (х + у) + z = х + (у + z), докажем, что (х + у) + z' = х + (у + z'). Имеем

(х + у) + z'=/опр. сложения п.2)/= ((х + у) + z)'=/предположение индукции/=

=(х + (у + z))'=/опр. сложения п.2)/= х + (у + z)'=/опр. сложения п.2)/= х + (у + z').

Ч. т. д.

 

Теорема 2.Операция сложения на множестве натуральных чисел коммутативна, т.е.

х, у N х + у = у +х.

Теорема 3. Для любых натуральных чисел х и у имеет место неравенство:

х+у ≠ х.

Теорема 4.Для любых натуральных чисел х, у, z если у ≠ z, то у + х ≠ z + х.

Доказательства теорем 2-4 проводят аналогично доказательству теоремы 1.