Главная | Обратная связь

Принципы расширения

Пусть построена некоторая система F₁ и требуется построить некоторую систему F₂, которое должно удовлетворять следующим принципам:

1) .

2) В F₂ должны выполняться все операции, которые выполнимы в F₁ , причем их смысл должен быть один и тот же, то есть результат выполнения операций в F₁ и F₂ должен быть одинаков, если на него смотреть как на элемент из F₂ .

3) В F₂ должна быть некоторая операция, которая в F₁ либо не выполняется, либо выполняется частично.

4) F₂ должно быть минимальной системой, удовлетворяющей 1-3.

Будем считать, что система натуральных чисел в N уже построена.

Определение 1. Кольцом целых чисел называется минимальное кольцо, содержащее N в качестве своего подполукольца.

Определение 1 согласуется с принципами расширения 1-4. Действительно, при F₁=N и при F₂= Z получаем:

1) NÍZ

2) В Z выполняется операции “+” “ ” , причем их смысл одинаков.

3) В Z выполняется операция вычитания, то есть сложение с противоположным элементом, а в N эта операция выполняется частично.

4) Z- минимальная система, удовлетворяющая 1-3.

Для того, чтобы доказать, что множество целых чисел существует, его нужно построить, то есть построить его модель.

Рассмотрим множество N´N. Оно состоит

На множестве введем отношение .

Определение 2. Упорядоченные пары (a,b) и (c,d) из называются равносильными и обозначают (a,b) ~ (c,d), если a+d=b+c.

Таким образом

Лемма 1. Отношение ~ на множестве является отношением эквивалентности.

Доказательство.

1. Рефлексивность. 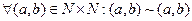, так как a+b=b+a.

2. Симметричность.

Пусть

3. Транзитивность.

Пусть Покажем, что

Из 1 следует, что a+d=b+c

Из 2 следует, что c+n=d+m

Из 1-3 следует, что отношение ~ является отношением эквивалентности.

По основной теореме об отношении эквивалентности множество разбивается отношением ~на непересекающиеся классы.

Определение 3. Множество ( по отношению ~) всех классов эквивалентности, на которые разбивается множество отношением ~, обозначается Z и называется множеством целых чисел, а его элементы называются целыми числами.