Главная | Обратная связь

Рационального числа в виде отношения целого числа к натуральному.

Определение 1. Рациональное число называется меньшим рационального числа 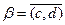, если .

Лемма 1. Отношение < на множестве ℚ определено корректно.

Доказательство. Пусть ~ (1), ~ (2) и 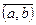< (3). Покажем, что < (4). Для доказательства (4) достаточно показать, что (5). Докажем (5):

из (1) (1'), из (2) 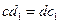(2'), из (3) (3').

Умножая равенство (3') на b₁>0, получим , отсюда, с учетом (1'), имеем , разделив обе части неравенства на b>0, получим: (4).

Заметим, что с учетом равенства (2') и d>0, d₁>0, числа с и с1 могут либо быть одновременно положительны, либо одновременно отрицательны, либо одновременно равны нулю.

Далее, возможны 3 случая:

1) с>0, с₁>0. Умножая (4) на с₁, получим , откуда, с учетом (2') , разделив это неравенство на с, получим (5).

2) с<0, с₁<0. Умножая (4) на с₁, получим 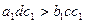, откуда, с учетом (2') , разделив это неравенство на с, получим (5).

3) с=0, с₁=0. Тогда, и умножая на d₁ и деля на d получим

Лемма доказана.

Лемма 2. Алгебраическая система <ℚ, < > является линейно упорядоченным множеством.

Теорема 1. Алгебраическая система < ℚ,+, · , < > является упорядоченным полем.

 

§19..Дальнейшие свойства рациональных чисел.

Построение множества действительных чисел мы будем осуществлять, считая известным множество рациональных чисел, перечисляя лишь основные свойства рациональных чисел.

На множестве рациональных чисел определены две операции – сложение и умножение, причем для любых рациональных чисел a, b, c выполняются следующие условия:

Ι.1. a+b=b+a

Ι.2. a+(b+c)=(a+b)+c

Ι.3. a+0=a

Ι.4. Для любого рационального числа a существует рациональное число b такое, что a+b=0. Это число обозначается (-a) и называется числом, противоположным числу a. Таким образом a+(-a)=0

Ι.5. ab=ba

Ι.6. a(bc)=(ab)c

Ι.7. a·1=a

Ι.8. Для любого a≠0 существует число b такое, что ab=1. Это число обозначается 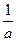и называется числом обратным числу a. Таким образом, a· 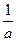=1, если a≠0.

На множестве рациональных чисел определены понятия положительного и отрицательного числа, причем выполняются следующие свойства:

Ι.10. Для любого рационального числа a имеет место одно и только одно: а) a=0 , б) a – положительное число, в) a – отрицательное число.

Ι.11. Сумма двух положительных чисел есть число положительное, произведение двух положительных чисел есть число положительное.

На множестве рациональных чисел вводится отношение порядка: полагают, что a больше b, и пишут a>b, если (a-b) – положительное число; если же (a-b) отрицательное число, то полагают, что a меньше b, и пишут a<b.

Отношение порядка удовлетворяет одному важному свойству, обычно называемому аксиомой Архимеда:

Ι.12. Для любых положительных чисел a и b найдется натуральное число N такое, что Na>b.

Из определения отношения порядка и свойств Ι.10-Ι.11 без труда получаются основные свойства числовых неравенств (для рациональных чисел):

2.1. Для любых рациональных чисел a и b имеет место одно и только одно из трех отношений: a>b, a<b, a=b.

2.2. Если a – положительное число, то a>0, если a отрицательное число, то a<0.

2.3. Если a>b, то b< a.

2.4. Если a>b, b>c, то a>c

2.5. Если a>b, то a+c>b+c

2.6. Если a>b, , то ac<bc

c>d, то a+c>b+d

2.7. Если a>b, c<d, то a-c>b-d.

2.8. Если a>b и c>0, то ac>bc

2.9. Если a>b и c<0, то ac<bc

2.10. Если a>b>0 и c>d>0, то ac>bd

2.11. Если a>b>0, то < .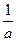

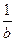Ниже приводятся некоторые дальнейшие утверждения и определения.

Лемма 1.Во всяком конечном множестве рациональных чисел есть наибольший и наименьший элементы.

Доказательство легко получается методом математической индукции.

Определения модуля (абсолютной величины) рационального числа:

=

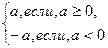
Основные свойства модулей рациональных чисел:

3.1.

3.2.

3.3.

3.4.

3.5.

3.6.

3.7.

3.8.

Определение ограниченного множества.

Определение 1.Множество А рациональных чисел называется ограниченным сверху (снизу), если существует рациональное число r такое, что для любого a A выполняется неравенство a<r (a>r). Множество, ограниченное и сверху, и снизу называется ограниченным.

В дальнейшем для удобства будем использовать кванторы. Например, определение ограниченности множества сверху с помощью кванторов запишется так: ( .

Приведенное в определении 1 условие равносильно следующему

(

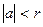
Введенные понятия можно распространить на последовательности рациональных чисел. Например, последовательность (в дальнейшем мы будем писать кратко ) называется ограниченной сверху, если

Определение 2.Последовательность рациональных чисел называется бесконечно малой, если

Условимся для краткости, вместо фразы «бесконечно малая последовательность рациональных чисел», писать БМ.

Самым простым примером БМ является стационарная последовательность , то есть последовательность, состоящая из одних нулей: 0,0,0,…,0,… .

Лемма 2.Сумма двух БМ есть БМ.

 

§20.. Фундаментальные последовательности рациональных чисел.

Определение 3.Последовательность рациональных чисел называется фундаментальной, если

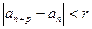
Условимся для краткости, вместо фразы «фундаментальная последовательность рациональных чисел», писать ФП. Самым простым примером ФП является стационарная последовательность . Всякая БМ также является фундаментальной.

В самом деле, пусть - БМ и r >0. Тогда

Далее имеем:

и фундаментальность последовательности доказана.

Отметим некоторые свойства фундаментальных последовательностей.

Теорема 1.Всякая ФП является ограниченной последовательностью.

Доказательство. Пусть - ФП. Тогда . Так как , то получаем .

По лемме 1, в конечном множестве 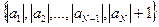есть наибольший элемент, обозначим его М. Тогда имеем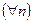 , а это означает ограниченность последовательности .

Теорема 2. Сумма двух ФП есть ФП.

Доказательство. Пусть - ФП, - ФП и . Покажем, что - ФП. Зададимся числом r > 0. Из фундаментальности последовательностей и получаем соответственно:

Положим 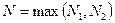, тогда для любого p будем иметь:

. Таким образом - ФП

Теорема 3.Произведение двух ФП есть ФП.

Доказательство. Пусть - ФП, - ФП и . Покажем, что - ФП. Заметим, прежде всего, что из фундаментальности последовательностей и следует по теореме 1 их ограниченность. Значит,

, .

Зададимся числом r >0. Из фундаментальности последовательностей и получаем, соответственно:

Если положить 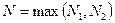, то при получим:

Итак, , а это означает, что - ФП.

Следствие 1.Если - ФП, а с - рациональное число, то - Фп.

Следствие 2.Если - ФП, то - ФП.

Следствие 3.Разность двух ФП есть ФП.

Нам осталось рассмотреть вопрос о делении фундаментальных последовательностей. Предварительно сформулируем и докажем важную лемму.

Лемма 3.Пусть - ФП не являющаяся бесконечно малой. Тогда существуют рациональное число d>0 и натуральное число N, такие, что последовательность удовлетворяет одному из двух условий:

1.

2.

Доказательство. Так как , по условию, последовательность не является БМ, то . Иными словами, бесконечное множество членов последовательности удовлетворяет неравенству (1).

Докажем, что, с другой стороны, неравенству удовлетворяет лишь конечное множество членов последовательности.

Предположим противное, что неравенству (2) удовлетворяет бесконечное множество членов последовательности . Из фундаментальности последовательности получаем:

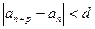(3).

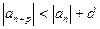Так как, кроме того , то (4).

Мы предположили, что неравенству (2) удовлетворяет бесконечное множество членов последовательности . Поэтому найдется номер такой, что (5).

Из неравенства (4) следует, что , а из неравенства (5) получаем, что . Но это означает, что неравенству (1) может удовлетворять лишь конечное множество членов последовательности (лишь члены с номерами, не превосходящими ), а это противоречит сказанному выше о неравенстве (1).

Итак, неравенству (2) удовлетворяет лишь конечное множество членов последовательности . Пусть - наибольший из номеров членов последовательности , которые удовлетворяют неравенству (2). Тогда для n> и тем более (6).

Покажем, что, начиная с номера , все члены последовательности либо положительны, либо отрицательны. Предположим, что это не так, то есть, что существуют n≥N и m≥N такие, что и имеют разные знаки, например, >0, <0. Так как , то из неравенства (3) получаем , то есть (7).

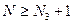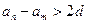С другой стороны, так как , то из неравенства (6) получаем и , то есть , а . В таком случае , а это противоречит неравенству (7).

Итак, начиная с номера N, все члены последовательности либо положительны, либо отрицательны, значит либо , либо . Лемма доказана.

В дальнейшем нам часто придется иметь дело с фундаментальными последовательностями рациональных чисел, не являющимися бесконечно малыми и не содержащими членов, равных 0. такие последовательности условимся называть регулярными.

Лемма 4.Если - регулярная последовательность, то существует такое положительное рациональное число e, что .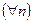

Доказательство. регулярная последовательность удовлетворяет условиям леммы 3, поэтому .

Положив , получаем для любого n, что и требовалось доказать.

Теорема 4.Если - регулярная последовательность, то - ФП.

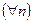
Доказательство. По лемме 4 . Зададимся рациональным числом r>0. Из фундаментальности последовательности получаем:

.

Тогда при n≥N и всех p , а это означает фундаментальность последовательности .

Следствие.Если - ФП, а - регулярная последовательность, то - ФП.

Это без труда получается из теорем 3и 4.