 |
|
Отношение эквивалентности на множестве фундаментальных последовательностей рациональных чисел.
Определение 4.Две фундаментальные последовательности  и
и  назовем эквивалентными и будем писать
назовем эквивалентными и будем писать  ~
~  , если
, если  - бесконечно малая последовательность.
- бесконечно малая последовательность.
Легко показать, что введенное таким образом на множестве ФП бинарное отношение рефлексивно (  ~
~  ), симметрично ( если
), симметрично ( если  ~
~  , то
, то  ~
~  ) и транзитивно ( если
) и транзитивно ( если  ~
~  и
и  ~
~  , то
, то  ~
~  ), а поэтому является отношением эквивалентности. Примером эквивалентных последовательностей могут служить любые две БМ.
), а поэтому является отношением эквивалентности. Примером эквивалентных последовательностей могут служить любые две БМ.
В следующих ниже теоремах отмечаются некоторые свойства эквивалентных последовательностей (мы рассматриваем только ФП).
Теорема 5.Если  ~
~ 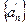 и
и  ~
~  , то
, то 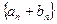 ~
~  .
.
Доказательство. Именно  . Значит, по лемме 2,
. Значит, по лемме 2,  - БМ. Этим эквивалентность последовательностей
- БМ. Этим эквивалентность последовательностей 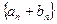 и
и  доказана.
доказана.
Теорема 6. Если  ~
~ 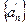 и
и  ~
~  , то
, то  ~
~  .
.
Доказательство. Положим 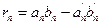 . Мы должны показать, что
. Мы должны показать, что  - БМ. Имеем
- БМ. Имеем  . Итак,
. Итак,
 (1).
(1).
Далее, по теореме 1, из фундаментальности последовательностей  и
и  следует их ограниченность, то есть
следует их ограниченность, то есть

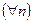
 (2)
(2)
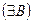
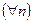
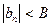 (3)
(3)
Зададимся теперь произвольным рациональным числом r>0. По условию  ~
~ 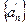 ,
,  ~
~  , следовательно
, следовательно 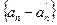 - БМ,
- БМ, 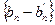 - БМ. Тогда
- БМ. Тогда


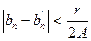 , (4)
, (4)

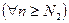
 . (5)
. (5)
Пусть 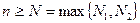 . Из неравенства (1), (2), (3), (4), (5), получаем
. Из неравенства (1), (2), (3), (4), (5), получаем  .
.
Итак 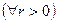


 . Значит,
. Значит,  - БМ и теорема доказана.
- БМ и теорема доказана.
Теорема 7. если в фундаментальной последовательности  отбросить первые
отбросить первые  членов, то оставшаяся последовательность будет эквивалентна исходной.
членов, то оставшаяся последовательность будет эквивалентна исходной.
Доказательство. Положим 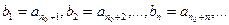 . Ясно , что
. Ясно , что  - ФП. Зададимся произвольным числом r>0. Из фундаментальности
- ФП. Зададимся произвольным числом r>0. Из фундаментальности  следует:
следует: 


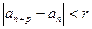 . В частности при n≥N,
. В частности при n≥N,  , то есть
, то есть 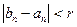 . Но это все и означает, что
. Но это все и означает, что 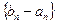 - БМ.
- БМ.
Из доказанной теоремы и леммы 3 следует:
Теорема 8. Пусть  - ФП, не являющаяся бесконечно малой. Тогда существуют регулярная последовательность
- ФП, не являющаяся бесконечно малой. Тогда существуют регулярная последовательность  и рациональное число d>0 такие, что все члены последовательности
и рациональное число d>0 такие, что все члены последовательности  либо положительны и больше d, либо отрицательны и меньше –d и
либо положительны и больше d, либо отрицательны и меньше –d и  ~
~  .
.
§4. Определение действительного числа.
Произведем разбиение множества всех ФП на классы по введенному выше отношению эквивалентности. Тогда каждый класс будет представлять собой множество эквивалентных друг другу ФП, а если последовательности взяты из разных классов, то эти последовательности не эквивалентны. Примером класса может служить класс бесконечно малых последовательностей.
Определение 5. Припишем каждому классу эквивалентных ФП свой символ. Этот символ назовем действительнымчислом, определенным данным классом.
Определение 6.Пусть  и
и 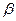 - действительные числа, определяемые, соответственно, классами А и В. Полагаем
- действительные числа, определяемые, соответственно, классами А и В. Полагаем  =
= 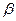 тогда и только тогда, когда А=В.
тогда и только тогда, когда А=В.
Определение 7. Пусть  и
и 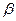 - действительные числа, определяемые, соответственно, классами А и В. Пусть
- действительные числа, определяемые, соответственно, классами А и В. Пусть  ,
,  , C – класс, которому принадлежит последовательность
, C – класс, которому принадлежит последовательность 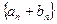 , а D класс, которому принадлежит последовательность
, а D класс, которому принадлежит последовательность  . Тогда действительное число, определяемое классом C, называется суммой чисел
. Тогда действительное число, определяемое классом C, называется суммой чисел  и
и 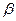 и обозначается
и обозначается  +
+ 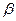 , а действительное число, определяемое классом D называется произведением чисел
, а действительное число, определяемое классом D называется произведением чисел  и
и 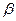 и обозначается
и обозначается 
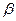 .
.
Это определение корректно, так как по теоремам 2 и 3 последовательности 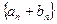 и
и  фундаментальны, то есть принадлежат некоторым классам ФП, по теоремам 5 и 6, классы C и D не будут зависеть от выбора конкретных представителей в классах А и В.
фундаментальны, то есть принадлежат некоторым классам ФП, по теоремам 5 и 6, классы C и D не будут зависеть от выбора конкретных представителей в классах А и В.
Пусть А – некоторый класс ФП. В этом классе не может быть более одной стационарной последовательности так как, если  и
и 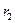 - различные рациональные числа, то
- различные рациональные числа, то  не является БМ. Итак, в классе А либо есть одна стационарная последовательность
не является БМ. Итак, в классе А либо есть одна стационарная последовательность  , либо нет ни одной стационарной последовательности. В первом случае отождествим действительное число, определяемой классом А, с рациональным числом r. Ясно, что в применении к рациональным числам получаются обычные определения суммы и произведения.
, либо нет ни одной стационарной последовательности. В первом случае отождествим действительное число, определяемой классом А, с рациональным числом r. Ясно, что в применении к рациональным числам получаются обычные определения суммы и произведения.
Отметим свойства операций сложения и умножения действительных чисел (эти числа будем обозначать греческими буквами).
1)  +
+ 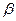 =
= 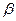 +
+  ,
,
2)  +(
+( 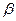 +
+  )=(
)=(  +
+ 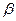 )+
)+  ,
,
3) 
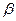 =
= 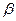
 ,
,
4)  (
( 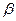
 )=(
)=( 
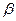 )
)  ,
,
5)  (
( 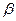 +
+  )=
)= 
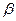 +
+ 
 ,
,
6)  +0=
+0=  .
.
Эти свойства непосредственно следуют из соответствующих свойств операций сложения и умножения на множестве рациональных чисел. Рассмотрим для примера доказательство свойства дистрибутивности.
Пусть  , такую запись следует понимать так: действительное число
, такую запись следует понимать так: действительное число  определяется классом, которому принадлежит ФП
определяется классом, которому принадлежит ФП  . Пусть далее
. Пусть далее  и
и  . Тогда, по определению 7,
. Тогда, по определению 7, 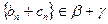 , а
, а 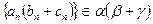 .
.
С другой стороны  _ Но an( bn+ cn)=anbn+ancn , то есть последовательность {an(bn+cn)} и {anbn + ancn} совпадают. Тогда и классы, содержащие эти последовательности, совпадают, то есть
_ Но an( bn+ cn)=anbn+ancn , то есть последовательность {an(bn+cn)} и {anbn + ancn} совпадают. Тогда и классы, содержащие эти последовательности, совпадают, то есть
α (β + γ) =αβ + αγ
7) Для любого числа α найдется число β такое, что
α + β= 0
В самом деле, пусть {an} 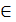 α , а β – число, определяемое классом, которому принадлежит {-α}. Так как {an+ (-an)}= {0}, то α + β=0.
α , а β – число, определяемое классом, которому принадлежит {-α}. Так как {an+ (-an)}= {0}, то α + β=0.
Число β обозначается –α называется числом, противоположным числу α. Значит , α +(-α)=0. Разностью действительных чисел α и β называется число α+(-β).
8) α*1=α
Для доказательства этого свойства достаточно в качестве представителя класса, определяющего число α, взять отрицательную последовательность {1}.
9) Для любого α≠0 существует число β такое, что
α*β=1
В самом деле, 0- это число , определяемое классом, которому принадлежит последовательность {0}. Тому же принадлежит и любая БМ. Следовательно, ввиду α≠0 никакая последовательность из класса, определяющего число α , не является БМ. Тогда по теореме 8 существует регулярная последовательность {an}  α, откуда по теореме 4, {1/an} – ФП. Пусть число определяемое классом, которому принадлежит {1/an}. Так как {an*(1/an)}= {1} , то α*β=1 .
α, откуда по теореме 4, {1/an} – ФП. Пусть число определяемое классом, которому принадлежит {1/an}. Так как {an*(1/an)}= {1} , то α*β=1 .
Число β обозначается 1/α и называется числом, обратным числу α. Теперь мы можем говорить о делении действительных чисел: если β≠0, то частным от деления α на β называется число α*(1/β).
§22.. Упорядоченность множества действительных чисел.
Определение 8.Пусть α≠0 и А – класс, определяющий число α. Если в классе А есть последовательность, состоящая только из положительных рациональных чисел, то α называется положительным действительным числом. Если в классе А есть последовательность, состоящая из одних отрицательных рациональных чисел, то α называется отрицательным действительным числом.
Теорема 9. Для любого действительного числа α имеет место одно и только одно из трех соотношений : α=0, α-положительное число,α- отрицательное число.
Д о к а з а т е л ь с т в о.
Пусть дано действительное число α≠0. Тогда в классе, определяющем число α, существует последовательность, состоящая только из положительных или только из отрицательных рациональных чисел – это вытекает из теоремы 8.
Достаточно поэтому показать, что в этом классе не может быть двух последовательностей таких, что все члены одной последовательности положительны, а все члены другой – отрицательны.
Предположим, что {an} 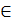 α, {bn}
α, {bn}  α и пусть (
α и пусть (  n) an >0. (
n) an >0. (  n) bn <0. По лемме 3 имеем
n) bn <0. По лемме 3 имеем
( 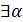 1>0) (
1>0) (  N1) (
N1) (  1) an >
1) an >  1,
1,
( 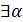 2>0) (
2>0) (  N2) (
N2) (  2) bn >
2) bn >  2
2
Положим N=max(N1N2), r= 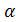 1 +
1 + 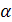 2. Тогда
2. Тогда
(  ) an - bn > r
) an - bn > r
Это значит , что { an - bn } не является БМ, то есть последовательности {an} и {bn} не эквивалентны и не принадлежат одному и тому же классу.
Полученное противоречие доказывает теорему.
Формально нужно еще показать, что α+β≠0 и α*β≠0.
Теорема 10. Если α и β- положительные действительные действительные числа, то α+β то и α*β – положительные числа.
Для доказательства достаточно в классах, определяющих числа α и β, выбрать последовательности, состоящие из одних положительных членов.
Определение 9. Пусть α и β – различные действительные числа. Говорят, что α больше β (и пишут α>β), если (α - β) - положительное число. Говорят , что α меньше β (и пишут α < β), если (α - β) отрицательное число.
Из определения 9 и теорем 9, 10 формально - логически без труда получаются основные свойства числовых неравенств для действительных чисел, аналогичные свойствам 2. 1- 2.11 из § 1. Особо остановимся на доказательстве свойства 1, 12(аксиомы Архимеда).
Теорема 11. Для любых положительных чисел α и β существует натуральное число N такое, что Nα>β.
Д о к а з а т е л ь с т в о.
Так как α- положительное число, а значит, класс А, определяющий число α, не содержит бесконечно малых последовательностей , то, по теореме 8 существует рациональное число d>0 и последовательность {an} 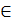 α такие, что (
α такие, что ( 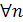 ) an >
) an >  (1).
(1).
Далее, возьмем в классе В , определяющем число β, последовательность {bn}, состоящую из одних положительных членов. По теореме 1, последовательность {bn}- ограниченна, значит:
(  М>0) (
М>0) ( 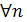 ) bn < M (2)
) bn < M (2)
Для положительных рациональных чисел  и М+ 1 справедливо свойство 1.12 из § 1аксиома Архимеда, то есть Существует натуральное число n такое, что
и М+ 1 справедливо свойство 1.12 из § 1аксиома Архимеда, то есть Существует натуральное число n такое, что 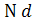 < М+ 1 (3).
< М+ 1 (3).
Рассмотрим теперь последовательность {cn} такую , что cn=Nan - bn, она фундаментальная по следствиям 1 и 3 теоремы 3. Из неравенств (1),(2),(3) следует , что Nan - bn > Pd- M>1.
Итак, ( 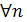 )сn> 1. Значит {cn} - регулярная последовательность с положительными членами, Тогда число γ=N d-β, определяемое классом, которому принадлежит последовательность {cn} , положительно. Значит N d > β что и требовалось доказать.
)сn> 1. Значит {cn} - регулярная последовательность с положительными членами, Тогда число γ=N d-β, определяемое классом, которому принадлежит последовательность {cn} , положительно. Значит N d > β что и требовалось доказать.