Главная | Обратная связь

Дальнейшие свойства неравенств натуральных чисел

Теорема 1. Для любого натурального числа n не существует такого натурального числа а, что n<a<n+1, т.е. n<a ⇒ n+1 .

Доказательство. Пусть n<a. Допустим, что a<n+1. Тогда по определению отношения < существует k 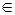ℕ, такое, что n+1=k+1. Если k=1, то n+1=a+1 ⇒ n=a, что невозможно. Пусть . Тогда по теореме 1 существует единственное число 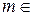ℕ, такое, что m′=k. Поэтому n+1=a+m′=a+m+1=(a+m)+1 ⇒ n=a+m и по определению n>a, что невозможно. Следовательно, n+1 a. Теорема доказана.

Теорема 2 (аксиома Архимеда). ∀a,b∈ℕ существует n∈ℕ такое, что a<nb.

Доказательство. Для любого a∈ℕ существует n∈ℕ такое, что a<n. В самом деле, в качестве n можно взять натуральное число a′=a+1. Отсюда следует, что a<a+1. По теореме 5′ ∀b∈ℕ : 1 b. Тогда почленно перемножая неравенства 1 b и 1<n,получаем 1‧a<b‧ n или a<bn. Теорема доказана.

Теорема 3. Любое непустое подмножество множества ℕ содержит наименьший элемент.

Доказательство. Пусть В⊆ℕ и В≠∅. Если 1∈ℕ, то по теореме 4′ 1 – наименьшее натуральное число в ℕ, и, тем более, в В. Пусть 1∉В и М – множество всех натуральных чисел, каждое из которых меньше любого натурального числа из В. Тогда М⊆ℕ. Покажем, что 1∈М. Действительно, так как 1∉В, то, в силу выбора множества М, получаем, что 1∈М.

Допустим, что из k∈M ⇒ k′∈M. Тогда по аксиоме (Р4) М=ℕ. Отсюда следует, что В=∅, что невозможно. Таким образом, существует n∈M такое, что n′∉M. Так как n<b, ∀ b∈B, то по теореме 5′ n′≤b, ∀ b∈B. Допустим, что n′<b, ∀ b∈B. Тогда по построению М имеем n′∈M, что невозможно. Следовательно, существует b₁∈B такое, что n′= b₁. Так как n′≤b, ∀ b∈B, то b₁≤b, ∀ b∈B, и значит, b₁ – наименьшее натуральное число в В. Теорема доказана.

Следствие 1. Для любого непустого подмножества В множества ℕ существует элемент b₁∈B, который непосредственно не следует ни за одним элементом из В, т.е. не существует с∈B, такого, что с′= b₁.

Доказательство. По теореме 7′ в В существует наименьший элемент b₁. Допустим, что существует с∈B, такой, что с′= b₁. Тогда с+1= b₁ и по определению 37 c< b₁, что невозможно. Следовательно, не существует с∈B, такого, что с′= b₁. Следствие доказано.

Теорема 4. Алгебраическая система <ℕ ,< > является вполне упорядоченным множеством.

Доказательство. По свойству 2 отношение < транзитивно на ℕ. Так как а≮а, ∀а∈ℕ, то отношение < антирефлексивно на ℕ. Из транзитивности и антирефлексивности следует свойство антисимметричности. Таким образом, отношение < является отношением порядка на ℕ. По свойству 1 отношение < является связанным, и значит, < - отношение линейного порядка. Следовательно, <ℕ,< >- линейно упорядоченное множество. Так как по теореме 3 любое непустое подмножество из ℕ имеет наименьший элемент, то <ℕ ,< >- вполне упорядоченное множество. Теорема доказана.

Теорема 9′. Алгебраическая система <ℕ , +, ‧ , < > является линейно упорядоченным полукольцом.

Доказательство. По теореме 13 <ℕ , +, ‧ >- полукольцо. По теореме 8′ <ℕ ,< >- вполне упорядоченное, а значит, линейно упорядоченное множество. Кроме того, в ℕ выполняются законы монотонности для сложения и умножения. Тогда, <ℕ , +, ‧ , < >- линейно упорядоченное полукольцо. Теорема доказана.