 |
|
Умножение целых чисел и его свойства
Определение 1. Произведением целых чисел  называется целое число
называется целое число  .
.
Лемма 1. Операция умножения целых чисел определена корректно, т.е. результат умножения не зависит от выбора представителей классов эквивалентности.
Доказательство.
Пусть (a,b)~(a1,b1) (1) и (c,d) ~(c1,d1) (2).
Докажем, что  =
=  (3).
(3).
Доказательство проведем в два этапа:
1-й этап - докажем, что  =
=  (4).
(4).
2-й этап – докажем что  =
=  (5).
(5).
1-й этап.
Для доказательства (4) достаточно показать, что  (6).
(6).
Для доказательства (6) достаточно показать, что (ac+bd,ad+bc)~ (a1c+b1d,a1d+b1c) (7).
Для доказательства (7) достаточно показать, что ac+bd+a1d+b1c= ad+bc+a1c+b1d (8).
Докажем (8).
Из 1)  a+b1=b+a1 (1')
a+b1=b+a1 (1')
ac+b1c=bc+a1c (9)
Из 1')  b+a1=a+b1 (1'')
b+a1=a+b1 (1'')
bd+a1d=ad+b1d (10)
(9) + (10)  (8)
(8)  (7)
(7)  (6)
(6)  (4)
(4)
Таким образом, равенство (4) верно.
2-й этап.
Для доказательства (5) достаточно показать, что
 (11).
(11).
Для доказательства (11) достаточно показать, что (ac+b1d,a1d+b1c)~ (a1c1+b1d,a1d+b1c1) (12).
Для доказательства (12) достаточно показать, что a1c1 + b1c1= b1d1+a1b1 (13).
Докажем (13).
Из 2)  c+d1=d+c1 (2')
c+d1=d+c1 (2')
a1c+a1d1=da1+a1c1 (14)
Из 2')  d+c1=c+d1 (2'')
d+c1=c+d1 (2'')
d1b+c1b1=cb1+d1b1 (15)
(14)+(15)  (13)
(13)  (12)
(12)  (11)
(11)  (5)
(5)
Таким образом равенство (5) верно.
Из (4) и (5)  (3). Лемма доказана.
(3). Лемма доказана.
Теорема 1. <Z ,∙> - абелев моноид.
Доказательство.
1) Из определения 42 и леммы 1  операция ∙ является алгебраической на Z.
операция ∙ является алгебраической на Z.
Так как 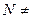 ø , то Z'≠0
ø , то Z'≠0  <Z',∙> - группоид.
<Z',∙> - группоид.
2) Покажем, что <Z,∙> - полугруппа.
Пусть α=(  ),
),  ,
, 
 Z.
Z.
Тогда  =(
=(  )
)  =
=  ,
,
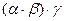 =
= 
 x=y
x=y  <Z,∙> - полугруппа.
<Z,∙> - полугруппа.
3) Покажем, что <Z,∙> - абелева полугруппа.
Пусть α=(  ),
), 
 Z.
Z.
 =(
=(  )
)  =
=  .
.
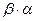 =
= 
 x=y
x=y  <Z,∙>- абелева полугруппа.
<Z,∙>- абелева полугруппа.
Покажем, что <Z,∙> - абелев моноид.
 ℮=
℮= 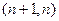
 Z, причем
Z, причем 
 Z:
Z:
 ℮=
℮= 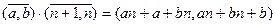 .
.
Покажем, что x=α.
Действительно, an + a+ n + n=an + bn + b + a  x=α.
x=α.
Из 1) и 4)  <Z,∙> - абелев моноид. Теорема доказана.
<Z,∙> - абелев моноид. Теорема доказана.
Теорема 2. <Z,+,∙> - кольцо ассоциативности с единицей.
Доказательство.
1. По теореме 33 <Z,+> - абелева группа.
2. По теореме 34 <Z,∙> - группоид.
3. Покажем, что в Z выполняются дистрибутивные законы.
Пусть α=(  ),
),  ,
, 
 Z. Тогда (α+β)γ=(a+c,b+d)∙(m,n)=
Z. Тогда (α+β)γ=(a+c,b+d)∙(m,n)=  ,
,
αγ+βγ=  +
+  =
= 
 x=y
x=y  выполняется правый дистрибутивный закон
выполняется правый дистрибутивный закон  выполняется левый дистрибутивный закон
выполняется левый дистрибутивный закон
Из 1)-3)  <Z,+,∙> - кольцо
<Z,+,∙> - кольцо  <Z,+,∙> - ассоциативное кольцо с единицей. Теорема доказана.
<Z,+,∙> - ассоциативное кольцо с единицей. Теорема доказана.
§15. Разбиение множества Z´N на классы эквивалентности. Множества рациональных чисел
Определение 1. Кольцом рациональных чисел называется минимальное поле, содержащее Z в качестве своего подкольца.
Определение 1 согласуется с принципами расширения 1-4. Действительно, при F1=Z и при F2= Q получаем:
1) ZÍQ
2) В Q выполняются операции “+” “·” и “–”, причем их смысл одинаков.
3) В Q выполняется операция деления, то есть умножение с обратным элементом, а в Z эта операция выполняется частично.
4) Q- минимальная система, удовлетворяющая 1-3.
Для того, чтобы доказать, что множество рациональных чисел существует, его нужно построить, то есть построить его модель.
Рассмотрим множество Z´N. Оно состоит

На множестве Z  N введем отношение ~.
N введем отношение ~.
Определение 2. Упорядоченные пары (a,b) и (c,d) из  называются равносильными и обозначают (a,b) ~ (c,d), если a·d=b·c.
называются равносильными и обозначают (a,b) ~ (c,d), если a·d=b·c.
Таким образом

Лемма 1. Отношение ~ на множестве  является отношением эквивалентности.
является отношением эквивалентности.
Доказательство.
4. Рефлексивность.  , так как a·b=b·a.
, так как a·b=b·a.
5. Симметричность.
Пусть 
6. Транзитивность.
Пусть  Покажем, что
Покажем, что 
Из 1 следует, что a·d=b·c
Из 2 следует, что c·n=d·m
a·d·c·n ·=b·c·d·m  a·n ·=b·m
a·n ·=b·m  3
3
Из 1-3 следует, что отношение ~ является отношением эквивалентности.
По основной теореме об отношении эквивалентности множество 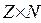 разбивается отношением ~ на непересекающиеся классы.
разбивается отношением ~ на непересекающиеся классы.
Определение 3. Множество  (по отношению ~) всех классов эквивалентности, на которые разбивается множество
(по отношению ~) всех классов эквивалентности, на которые разбивается множество  отношением ~, обозначается Q и называется множеством рациональных чисел, а его элементы называются рациональными числами.
отношением ~, обозначается Q и называется множеством рациональных чисел, а его элементы называются рациональными числами.