Главная | Обратная связь

Приклади розв’язування типових задач

Задача 1.1. Телефонна лінія, що з’єднує два пункти А і В, які розташовані один від одного на відстані 2 км, обірвалась у невідомому місці. Яка ймовірність, що обрив знаходиться не далі, ніж 450 м від пункту А?

Розв’язання. Нехай подія А: „обрив знаходиться не далі, ніж 450 м від пункту А”. Розклавши мисленно всю лінію на окремі метри, можна згідно реальної однорідності всіх цих ділянок, допустити, що ймовірність обриву однакова для кожного метру. Тому шукана ймовірність дорівнює

Р(А) = 450:2000 = 0,225.

Відповідь: 0,225.

 

Задача 1.2. З 16 учнів, серед яких 4 дівчини, на вечір зустрічі без вибору запрошують трьох учнів. Яка імовірність того, що серед запрошених буде одна дівчина?

Розв’язання. Нехай А – подія, імовірність якої шукається. Для визначення всіх елементарних подій слід знати, скільки різних груп по 3 учні з 16 можна утворити. Тут маємо справу з числом комбінацій з 16 елементів по 3, тобто n=С₁₆³. Щоб підрахувати кількість подій, які сприяють події А, зауважимо, що одну дівчину з чотирьох можна вибрати С₄¹ способами, а два інших учня мають бути хлопцями. Два хлопця з 12 можна вибрати С₁₂² різними способами. Оскільки треба запросити 1 дівчину і 2 хлопці, то всього таких груп буде С₄¹·С₁₂², тобто m = С₄¹·С₁₂².

Отже, Р(А) = = = .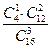

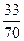Відповідь: 33/70.

 

Задача 1.3. Кожну букву, що входить у слово “вдосконалення” виписано на окрему картку. Яка імовірність того, що після ретельного перемішування й виймання п’яти карток отримаємо слово “скеля”?

Розв’язання. У сполуках з тринадцяти букв по п’ять, нас цікавлять букви і їх черговість (порядок). Отже, п = А₁₃⁵. З усіх випадків лише один сприяє появі слова “скеля”, тому т = 1. Шукана імовірність

Р(А) = = = = .

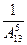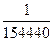Відповідь:1/154440.

 

Задача 1.4. Циліндричні прути радіуса r утворюють решітку з прямокутними отворами розміром а x b. На решітку, перпендикулярно до її поверхні, кидають кульку діаметром d. Яка ймовірність того, що кулька вільно пройде через отвори?

Розв’язання. Нехай А – подія, яка заключається у вільному проходженні кульки через отвори. Якщо d>a або d>b, то ймовірність проходження Р(А)=0.

В інших випадках ймовірність проходження кульки через решітку дорівнює ймовірності проходження кульки через один отвір решітки. Площа одного отвору решітки з урахуванням розмірів прутів =(a+2r)(b+2r). Для того, щоб кулька вільно пройшла через отвір, її центр повинен знаходитися від прутів на відстані, не меншій за d/2.

Таким чином, площа, яка сприяє вільному проходженню кульки, =(b-d)(a-d). Тоді

Р(А)= = .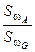

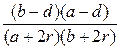Відповідь:1/154440.

Індивідуальні завдання для самостійної роботи

 

1. В лотереї з 50 квитків 8 виграшних. Яка ймовірність того, що серед 5 навмання придбаних квитків два будуть виграшними?

2. З 6 однакових карток розрізної азбуки: „а”, „е”, „м”, „н”, „о”, „р” навмання вибирають 4 картки й складають їх в ряд по рядку, яка ймовірність отримати при цьому слово „море”?

3. У ящику 36 деталей, 9 з них – браковані. Обчислити ймовірність того, що серед 7 взятих навмання деталей 3 буде бракованих.

4. На 6 однакових картках написано букви: „а”, „в”, „к”, „м”, „о”, „с”. Картки зміщують і розкладають навмання в ряд. Яка ймовірність того, що отрималося слово ”Москва”?

5. Із корзини, що містить 5 кульок, які помічені цифрами 1, 2, 3, 4, 5, витягають навмання всі кульки одну за одною. Яка ймовірність того, що номера витягнутих кульок йдуть у порядку зростання?

6. З нового набору доміно навмання витягують одну кісточку. Яка ймовірність того, що число вічок на ній парне?

7. З 60 екзаменаційних питань учень підготував 50. На екзамені він повинен відповісти на два питання. Яка ймовірність того, що учень відповість на обидва питання?

8. З 10 квитків лотереї виграшними є два. Яка ймовірність того, що серед взятих навмання 5-ти білетів два виграшні?

9. У корзині 6 білих і 9 чорних кульок. З корзини виймають одночасно дві кульки. Яка ймовірність того, що обидві кульки виявляться чорними?

10. У партії з 8 деталей є 6 стандартних. Яка ймовірність того, що серед п’яти взятих навмання деталей три стандартні?

11. Достатньою умовою здачі колоквіуму є відповідь на одне з двох заданих запитань. Студент не знає вісім питань із тих сорока, які пропонуються. Яка ймовірність здачі колоквіуму?

12. Яка ймовірність вгадати 4 номери у лотереї „Спортлото” 6 із 49?

13. У пакунку є 10 цукерок “Кара-кум” та 5 “Південна ніч”. Навмання беруть 6 цукерок. Яка ймовірність того, що серед них виявиться дві “Кара-кум”?

14. У ящику 50 деталей, 12 з них – браковані. Обчислити ймовірність того, що серед 6 взятих навмання деталей 2 буде бракованих.

15. Набираючи номер телефону, абонент забув 2 останні цифри і, пам’ятаючи тільки, що ці цифри різні, набрав їх навмання. Знайти ймовірність того, що набрано потрібні цифри.

16. Бібліотекар отримав 5 книг з синьою обкладинкою і 7 з жовтою. На полицю він навмання поставив 5 книг. Яка ймовірність того, що серед них будуть 2 книги з синьою обкладинкою і 3 з жовтою?

17. У книжному магазині на полиці лежать 20 книг, причому 10 книг коштують по 20 гривень кожна, 3 книги – по 40 гривень і 7 книг – по 10 гривень. Яка ймовірність того, що випадковим чином вибрані 2 книги коштують 30 гривень?

18. Десять книжок з теорії ймовірностей розставляють на полиці. Яка ймовірність того, що книги двотомника В.Феллера будуть поставлені поряд?

19. Гусениця трактора складається з 50 ланок. Перед тим, як її збирати, три ланки помітили цифрами „1”, „2”, „3”. Яка ймовірність того, що після ремонту гусениці ці ділянки виявляться поряд, причому нумерація буде розміщена в порядку зростання чисел?

20. На складі є 15 радіодеталей, причому 10 з них виготовлені чернівецьким радіозаводом, а 5 – кіровоградським. Яка ймовірність того, що серед 6 взятих навмання деталей 2 будуть виготовлені чернівецьким радіозаводом, а 3 – кіровоградським?

21. У бригаді 12 чоловік, серед яких 4 жінки. По списку навмання відібрано 9 чоловік. Знайти ймовірність того, що серед відібраних 6 чоловіків.

22. Яка ймовірність вгадати всі 6 номерів у лотереї „Спортлото” 6 із 49?

23. У ящику 46 деталей, 8 з них – браковані. Обчислити ймовірність того, що серед 5 взятих навмання деталей 3 буде бракованих.

24. Яка ймовірність вгадати 5 номерів у лотереї „Спортлото” 5 із 36?

25. Бібліотекар викладає на полицю 9 книг. Яка ймовірність того, що дві певні книги будуть стояти поряд?

26. Букви розрізної абетки „л”, „р”, „в”, „е”, „о”, „с” розкладають випадковим порядком у ряд. Яка ймовірність того, що у будь-якому місці ряду отримається слово „лев”?

27. Бібліотечка складається з 8 книг. 3 книги коштують по 30 гривень, 3 – по 10 гривень і 2 – по 20 гривень. Випадковим чином вибирають 2 книги. Знайти ймовірність того, що обрані книги коштують 40 гривень.

28. Автобуси Кіровоград-Київ та Київ-Кіровоград прибувають у Смілу між 10-ою і 11-ою годинами. Зупинка автобуса триває 15 хвилин. Яка ймовірність того, що автобуси зустрінуться на автовокзалі в м. Сміла?

29. Яка ймовірність того, що в „Спортлото” 6 із 49 правильно вгадані 3 номера?

30. Серед 30 екзаменаційних білетів 5 „щасливих”. Два студенти по черзі беруть по одному білету. Яка ймовірність того, що:

а) перший студент взяв „щасливий” білет;

б) другий студент взяв „щасливий” білет;

в) обидва студенти взяли „щасливі” білети?