Главная | Обратная связь

Приклади випробувань і відповідних їм випадкових подій.

 

№ п/п	Випробування	Випадкова подія
1.	Підкидання грального кубика	Поява чотирьох очок на верхній грані
2.	Гра в шахи	Виграш у суперника
3.	Випуск ламп заводом	Поява бракованої лампи

 

Якщо в результаті випробування подія обов’язково відбудеться, то вона називається вірогідною, а якщо не може відбутися, то – неможливою. Вірогідна подія позначається Ω, а неможлива – Ø. Наприклад, поява хоч одного із шести очок під час одного кидання грального кубика – вірогідна подія, а поява семи очок у цьому ж випробуванні – неможлива подія.

Теорія ймовірностей вивчає масові випадкові події. Масовими називають однорідні події, що спостерігаються за певних умов, які можуть бути відтворені необмежену кількість разів. Наприклад, влучення або промах у серії пострілів, поява бракованих виробів при серійному їх випуску, поява “числа” під час підкидання монети. Масовими вважають і ті події, для яких відповідні випробування не можна відтворити, але є можливість спостерігати аналогічні випробування у великій кількості. Наприклад, виклик телефонної станції абонентами, радіоактивний розпад атомів речовини тощо.

Означення. Множина подій утворює повну групу подій, якщо внаслідок кожного випробування хоч одна з цих подій напевно відбудеться. Наприклад: 1. Поява 1, 2, 3, 4, 5, 6 очок під час одного кидання грального кубика.

2. Виграш чи програш по даному лотерейному білету в певному тиражі.

3. Поява білої або червоної кулі під час виймання куль з урни, де є 5 білих і 3 червоні кулі.

Означення. Події А₁, А₂, ..., А_n називаються попарно несумісними в даному випробуванні, якщо ніякі дві з них не можуть відбутися разом. Наприклад: 1. Влучення і промах під час одного пострілу – несумісні події.
2. Поява 1, 2, 3, 4, 5, 6 очок під час одного кидання грального кубика – приклад множини з 6 несумісних подій.

Означення. Події, які можуть з’являтися одночасно, називають сумісними. Наприклад: випадання парного числа вічок і числа вічок, кратного трьом, при одному підкиданні кубика (6 – парне число, кратне 3).

Події А₁, А₂, ..., А_n можуть бути рівноможливими. Під рівноможливимирозуміють такі події , кожна з яких не має ніяких переваг у появі частіше за іншу під час багаторазових випробувань, що проводяться за однакових умов.

Наприклад: 1). Попадання даної команди в І, ІІ, ІІІ, IV групу під час жеребкування спортивних команд. 2). Поява 1, 2, 3, 4, 5, 6 очок під час одного кидання грального кубика.

Багато теоретичних тверджень теорії імовірностей будується на розгляді множини подій, які мають всі три властивості: утворюють повну групу подій, є несумісним і рівноможливими. Події такої множини називаютьсяелементарними. Наприклад:1) поява “ герба “ чи “числа “ під час одного кидання монети; 2) поява 1, 2, 3, 4, 5, 6 очок під час одного кидання грального кубика. Сукупність всіх елементарних подій називається простором елементарних подій і позначається грецькою буквою W.

Найважливішим поняттям теорії імовірностей як галузі математики є поняття імовірності випадкової події. Імовірність – це числова характеристика можливості появи випадкової події за певних умов, які можуть повторюватися необмежену кількість разів.

Класичне означення ймовірності. Імовірністю випадкової події називається відношення числа наслідків випробування (елементарних подій), які сприяють цій події, до загального числа всіх рівноможливих несумісних елементарних подій, які утворюють повну групу.

Тобто, ймовірність події А дорівнює

Р(А)= , (1.1)

де п – загальне число рівноможливих і несумісних елементарних подій, які утворюють повну групу, т – число елементарних наслідків, які сприяють події А. Причому Р(Ω)=1, Р(Ø)=0,

0£Р(А)£1. (1.2)

Безпосередній підрахунок ймовірностей подій значно спрощується, якщо для попереднього обчислення m і n використати формули комбінаторики. При цьому правильність розв’язування задачі залежить від уміння визначити вид сполук, що утворюються сукупністю подій, про які йдеться в умові задачі.

Якщо число наслідків випробування є нескінченим, то користуються геометричним означенням ймовірності. При цьому кожному елементарному наслідку ставлять у відповідність точку в деякій області G (у випадку, коли за простір елементарних подій Ω=ω_G береться просторове тіло). Ймовірність події А при цьому визначається виразом:

Р(А)= , (1.3)

де – об’єм області, при попаданні точки в яку подія точно відбудеться; – об’єм області, в яку точка обов’язково попаде під час проведення експерименту.

У випадку, коли G – відрізок, а події А відповідає точка, що належить частині цього відрізка, формула для обчислення ймовірності події А набуває вигляду:

Р(А)= , (1.4)

де 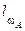– довжина відрізка, при належності точки якому подія точно відбудеться; – довжина відрізка, на який точка точно попаде в результаті проведення експерименту.

Коли G – плоска фігура, а події А відповідає точка, що належить частині цієї фігури, ймовірність події А обчислюють за формулою:

Р(А)= 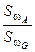, (1.5)

де – площа плоскої фігури, при належності точки якій подія точно відбудеться; – площа фігури, якій точка точно належатиме в результаті проведення експерименту.

Ймовірності, які визначаються формулами (1.3) – (1.5), називаються геометричними ймовірностями.

Класичне й геометричне визначення передбачають обчислення ймовірності до проведення експерименту. Якщо ж відомі результати експериментів, то ймовірність можна визначити як відношення числа експериментів, у яких подія відбулася, до загального числа проведених експериментів, якщо це число досить велике. Тобто за ймовірність події А наближено приймають її відносну частоту

Р(А)»ν(А). (1.6)

Це – статистичне (частотне) означення ймовірності.